 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Основне рiвняння динаміки обертального руху абсолютно твердого тiла
Розглянемо обертання АТТ навколо нерухомої точки О (нехай вона збiгається з центром мас) пiд дiєю зовнiшнiх сил  . Вiдповідно до виразу (2.39) його момент iмпульсу
. Вiдповідно до виразу (2.39) його момент iмпульсу

Продиференціюємо за часом цей вираз:
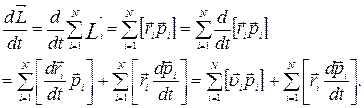
Оскiльки вектори 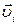 та
та  , колiнеарнi, їх векторний добуток дорiвнює нулю. Тодi з урахуванням формули (2.13) останнiй вираз стане:
, колiнеарнi, їх векторний добуток дорiвнює нулю. Тодi з урахуванням формули (2.13) останнiй вираз стане:
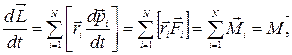
де 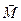 — головний момент зовнiшнiх сил, що дiють на АТТ.
— головний момент зовнiшнiх сил, що дiють на АТТ.
Остаточний вираз має вигляд:
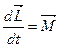 (2.42)
(2.42)
i називається основним рiвнянням динамiки обертального руху АТТ вiдносно нерухомої точки О.
Воно свiдчить про те, що похiдна моменту iмпульсу АТТ за часом дорiвнює головному моменту дiючих зовнiшнiх сил. (Моменти 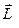 і
і 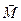 визначаються вiдносно однiєї й тiєї ж точки обертання О). Якщо АТТ обертається навколо нерухомої осi, то рiвняння (2.42) запишеться у вiдповiдних проекцiях
визначаються вiдносно однiєї й тiєї ж точки обертання О). Якщо АТТ обертається навколо нерухомої осi, то рiвняння (2.42) запишеться у вiдповiдних проекцiях 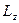 i
i  на цю вiсь:
на цю вiсь:
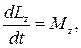 (2.43)
(2.43)
тобто похiдна за часом вiд моменту iмпульсу АТТ вiдносно нерухомої осi обертання дорiвнює головному моменту зовнiшнiх сил вiдносно цiєї осi.
Рiвняння (2.43) можна записати iнакше, якщо врахувати вирази (2.41) та (1.50), а також те, що момент iнерцiї I = соnst:

тобто
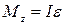 (2.44)
(2.44)
для обертання навколо нерухомої, осi.
Якщо тiло обертається навколо нерухомої точки О, останнiй вираз буде таким:
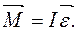 (2.45)
(2.45)
Цi вирази читаються так: добуток моменту iнерцiї АТТ вiдносно нерухомої точки (або осi) обертання на кутове прискорення дорiвнює головному моменту зовнiшнiх сил вiдносно тiєї ж точки (або осi) обертання.
Неважко побачити, що рiвняння (2.42) i (2.45) нагадують записи другого закону Ньютона для поступального руку (див. рiвняння (2.13) та (2.8)). Тiльки роль маси тут вiдiграє момент iнерцiї, роль сили — момент сили 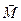 , роль iмпульсу — момент iмпульсу
, роль iмпульсу — момент iмпульсу 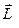 роль лiнійного прискорення — кутове прискорення
роль лiнійного прискорення — кутове прискорення 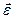 . Якщо при поступальному русi причиною змiни руху були дiючi сили
. Якщо при поступальному русi причиною змiни руху були дiючi сили 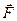 , то при обертальному русi причиною змiни обертання є момент дiючих сил
, то при обертальному русi причиною змiни обертання є момент дiючих сил 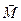 , причому чим вiн бiльший, тим швидше змінюється обертання.
, причому чим вiн бiльший, тим швидше змінюється обертання.
Поиск по сайту: