АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Обернена задача кiнематики

Читайте также:
  1. VI. Общая задача чистого разума
  2. Вопрос 2 Проверка и оценка в задачах со случайными процессами на примере решения задач экозащиты, безопасности и риска.
  3. Глава 10 Системный подход к задачам управления. Управленческие решения
  4. ГЛАВА 2.1. ЗАЩИТА ИННОВАЦИЙ КАК ЗАДАЧА УПРАВЛЕНИЯ ИННОВАЦИОННЫМИ ПРОЦЕССАМИ
  5. Глава 4. Математические основы оптимального управления в экономических задачах массового обслуживания
  6. Двойственная задача линейного программирования.
  7. Доклад о задачах власти Советов
  8. Доклад об экономическом положении рабочих Петрограда и задачах рабочего класса на заседании рабочей секции Петроградского совета рабочих и солдатских депутатов
  9. Задача 1
  10. Задача 1
  11. Задача 1
  12. Задача 1

Обернена задача кiнематики полягає в знаходженнi рiвняння руху за вiдомими характеристиками руху.

Розглянемо, як за вiдомими 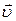i 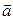можна знайти рiвняння руху в траєкторному виглядi 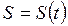. Запишемо з виразу (1.12) елементарний шлях, пройдений за час :

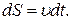(1.32)

Щоб знайти весь шлях, пройдений за певний промiжок часу 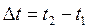, слід проiнтегрувати цей вираз:

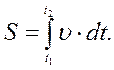(1.33)

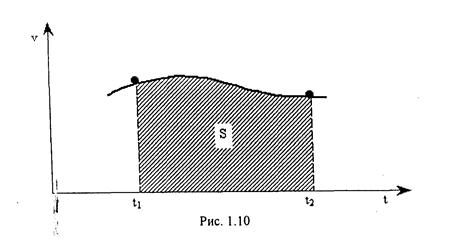
Графiчно цей iнтеграл зображений на рис. 1.10, з якого видно, що шлях чисельно дорiвнює площi фiгури (криволiнiйної трапеції), що обмежена кривою .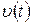

Аналогiчно за вiдомим прискоренням можна знайти швидкiсть у довiльний момент часу :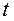

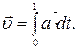(1.34)

Якщо в початковий момент часу 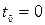, тiло мало початкову швидкiсть 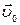, то

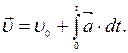(1.35)

Застосуємо наведенi вирази для рiвнозмiнного прямолiнiйного руху при 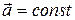. Тодi рiвняння (1.35) перепишеться:

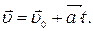(1.36)

З виразу (1.33) можна одержати:

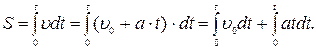
Остаточно:

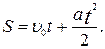(1.37)

Знайшовши 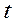з виразу (1.36) i пiдставивши його у вираз (1.37), можна одержати рiвняння, яке часто зручно використовувати в задачах:

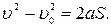(1.38)


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)