 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Перетворення Галiлея
Розглянемо точку Р, за якою ведеться спостереження одразу з двох iнерцiальних систем вiдлiку: К (х, у, z) та К’ (х’, у’, z’). Система К’ рухається вiдносно системи К зi швидкiстю υ «с вздовж осi ОХ. Виберемо осi координат так, як показано на рис.4.1.
Розглянемо спочатку випадок, коли точка Р нерухома в системi К. Вiдлiк часу почнемо з моменту, коли початки координат обох систем збiглися. Через якийсь час t’ координати точки Р в системi К’ будуть тi ж: х’, у’, z’, а в системi К координати будуть дорiвнюватi (рис.4.1):
 (4.1)
(4.1)
(Остання рівність t = t’ з’явилась тому, що в ньютонiвськiй механiцi час вважається абсолютним i однаковим в усiх системах вiдлiку).
Вираз (4.1) називається перетворенням Галілея. Вiн дозволяє перейти вiд координат i часу однiєї iнерцiальної системи вiдлiку до координат i часу iншої iнерцiальної системи.
Тепер розглянемо випадок, коли точка Р рухається з деякою швидкiстю  вiдносно системи К. Тодi значення її координат будуть змiнюватися з часом. Продиференцiюємо рiвнiсть (4.1) за часом:
вiдносно системи К. Тодi значення її координат будуть змiнюватися з часом. Продиференцiюємо рiвнiсть (4.1) за часом:
 (4.2)
(4.2)

Так ми одержали вирази для проекцiй швидкості точки в системi К i її зв’язок з проекцiями швидкостi в системi К¢

або у векторному виглядi маємо рiвняння:
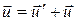 . (4.3)
. (4.3)
Цей вираз є класичним законом додавання швидкостей, який слiд читати так: швидкість точки вiдносно системи К дорiвнює векторнiй сумi швидкостей – швидкостi точки в системi К¢ i швидкостi самої системи К¢ вiдносно системи К.
Продиференцiювавши вираз (4.3) ще раз за часом, одержимо:
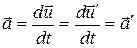 (4.4)
(4.4)
Це означає, що прискорення точки вiдносно обох iнерцiальних систем К i К’ однаковi, тобто прискорення є величина абсолютна. Тому, що маса точки вважається однаковою в усiх системах, можна записати:  . Тодi швидкостi змiни iмпульсу точки в обох системах також будуть однаковими:
. Тодi швидкостi змiни iмпульсу точки в обох системах також будуть однаковими:

Звiдси виходить, що й вимiряна величина сили, що дiє на точку, в обох системах теж буде однаковою, тому що


Це означає, що другий закон Ньютона однаково виконується i формулюється для всiх iнерцiальних систем вiдлiку. Те ж саме можна сказати про всi iншi закони механiки. Це твердження називається принципом вiдносностi Галiлея: неможливо будь-якими механiчними дослiдами, що проводяться в межах даної iнерцiальної системи вiдлiку, встановити,чи перебуває ця система у станi спокою, чи в станi рiвномiрного прямолiнiйного руху.
Величини, що мають однi й тi ж числовi значення в усiх системах вiдлiку, називаються iнварiантними (латинською незмiнними). Також iнварiантними називаються такi рiвняння, що не змiнюються в процесi перетворень координат i часу при переходi з однiєї iнерцiальної системи координат в iншу.
Тодi принцип вiдносностi Галiлея може бути сформульований так: рiвняння механiки iнварiантнi вiдносно до перетворень Галiлея.
Поиск по сайту: