Перетворення Лоренца та їх наслiдки

Для великих швидкостей, якi можна порiвнювати зi швидкiстю свiтла, замiсть перетворення Галiлея використовують перетворення Лоренца. Можна показати (без доведення), що для випадку, зображеному на рис. 4.1, перетворення Лоренца мають вигляд:

система К система К¢

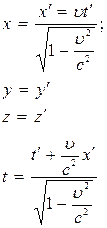
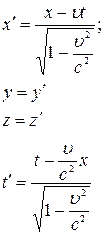
Розглянемо деякi наслiдки з перетворень Лоренца. При невеликих швидкостях υ -- с, перетворення Лоренца переходять у перетворення Галiлея. Дiйсно, в цьому разі 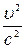=0, тоді 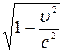=1; вираз (4.5) перетворюється на 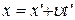а вираз (4.7) дає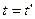

Замiсть класичного закону додавання швидкостей з перетворення Лоренца випливає релятивістський закон додавання швидкостей:

,

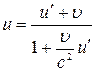де u — швидкiсть точки в системi К; u¢ — швидкiсть точки в системi К¢; υ - швидкiсть системи К¢ вiдносно системи К, дiйсно, за означенням 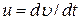. Використовуючи вирази (4.5), (4.7), знайдемо

,

Тоді

,

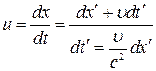Подiлимо чисельник i знаменник в цьому виразi на :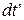

,

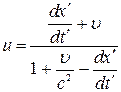i, врахувавши, що

.

одержимо формулу закону додавання швидкостей.

Звернемо увагу, що якщо покласти 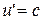i , то

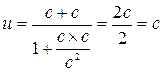
тобто релятивістський закон додавання швидкостей вiдповiдає другому постулату СТВ. Якщо ж швидкостi 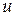, 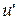та υ малi порiвняно зi швидкістю с, то 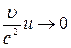, i релятивiстський закон додавання швидкостей перетворюється на класичний закон .

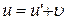Довжина тiла в рiзних системах вiдлiку виявляється рiзною (так зване скорочення довжини). Розглянемо стрижень, який розмiщено в ситемi К’, причому вiдносно К’ стрижень перебуває в станi спокою (рис.4.2). Позначимо його довжину 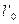(часто її називають власною довжиною). Якщо 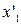i координати початку i кiнця стрижня, то

,

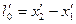Знайдемо довжину цього стрижня l вiдносно системи К, тобто системи, вiдносно якої вiн рухається. Зрозумiло, що , причому координати початку l кінця стриженя 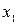і 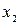мають бути вимiрянi одночасно. Використовуючи рiвняння (4.6) маємо

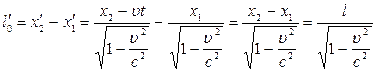
або (4.9)

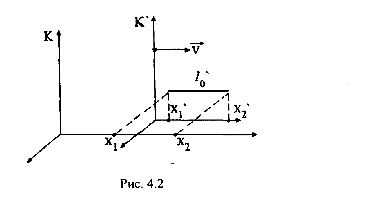
Отже, довжина тiла в системi, вiдносно якої воно рухається є меншою нiж довжина тiла в системi, вiдносно якої воно перебуває в станi спокою ().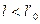

Часовий проміжок між двома подіями в різних системах виявляється різним (так зване уповільнення часу). Нехай у системі К¢ в однiй i тiй же точцi з координатами х¢ вiдбуваються двi подiї в моменти часу 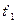i за годинником, що нерухомий вiдносно до системи К¢. Позначимо промiжок часу мiж цими подiями 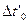(його часто називають власним часом):

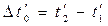
У системi К промiжок мiж цими подiями буде 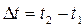, причому моменти 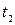і 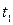вимiряються за годинником, що перебуває в системi К. Використовуючи вираз (4.7), одержимо:

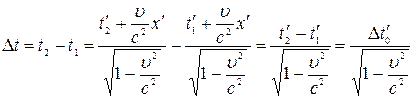
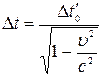, (4.10)

тобто 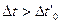.Це означає, що в рухомiй системi вiдлiку час уповiльнюється. А це дає змогу дійти загального висновку, що в рiзних iнерцiальних системах вiдлiку час плине по-рiзному.

Не можна окремо розглядати абсолютний простiр i абсолютний час як такi, що не пов’язанi мiж собою. Навпаки, простiр i час органiчно пов’язанi й утворюють єдину форму iснування матерії — простiр-час. Цей простiр-час має три просторовi координати (х, у,z) i одну часову (t), тобто є чотиривимiрний.

Поиск по сайту: