 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Момент сили
Моментом сили 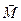 . або обертальним моментом вiдносно точки обертання О називається векторний добуток радiус-вектора
. або обертальним моментом вiдносно точки обертання О називається векторний добуток радiус-вектора  , проведеного з точки О в точку прикладання сили, на цю силу
, проведеного з точки О в точку прикладання сили, на цю силу 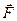 :
:
 (2.20)
(2.20)
Визначення моменту сили дано так, щоб кутове прискорення i кутова швидкiсть, якi виникають внаслiдок дiї моменту сили, збiгалися за напрямком з цим моментом. Тобто вектор 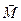 спрямований перпендикулярно площинi розташування векторiв
спрямований перпендикулярно площинi розташування векторiв  i
i 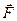 , вiдповiдно до правила правого гвинта (рис.2.3,а).
, вiдповiдно до правила правого гвинта (рис.2.3,а).
Модуль моменту сили дорiвнює:
 (2.21)
(2.21)
де 
 — кут мiж векторами
— кут мiж векторами  i
i 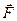 , а
, а  — перпендикуляр, проведений з точки О на лiнiю дiї сили
— перпендикуляр, проведений з точки О на лiнiю дiї сили 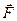 , який навивається плечем сили. Одиницею вимiрiв моменту сили є ньютон ×метр (Н м).
, який навивається плечем сили. Одиницею вимiрiв моменту сили є ньютон ×метр (Н м).
Якщо на тiло дiє кiлька сил, можна знайти суму моментiв цих сил відносно точки обертання О. Ця сума називається головним моментом зовнiшнiх сил вiдносно точки обертання О:

 (2.22)
(2.22)
Моментом сили вiдносно осi обертання z називають проекцiю вектора 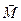 вiдносно точки обертання О на цю вiсь за умови, що вiсь проходить через цю точку О (рис. 2.3,б);
вiдносно точки обертання О на цю вiсь за умови, що вiсь проходить через цю точку О (рис. 2.3,б);
 (2.23)
(2.23)
Якщо вектор 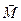 збігається за напрямком з вiссю, то його проекцiя дорiвнює модулю вектора
збігається за напрямком з вiссю, то його проекцiя дорiвнює модулю вектора 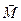 :
:
 (2.24)
(2.24)
Нехай на тiло дiють двi сили, якi рiвнi за модулем, а спрямованi протилежно вздовж паралельних прямих. Такi сили називаються парою сил (рис. 2.4).
Згiдно з виразом (2.20), момент пари сил вiдносно точки О

а його модуль
 (2.25)
(2.25)
 |
Оскільки
 то
то
 (2.26)
(2.26)
де l = l 1 +l 2 - плече пари, тобто найкоротша вiдстань мiж прямими, вздовж яких дiють сили одержаний вираз не залежить вiд розташування точки О.
Узагалі, щоб тiло, на яке дiють рiзнi зовнiшнi сили, не оберталося, тобто знаходилось в рiвновазi, сумарний момент цих сил має дорiвнювати нулю:
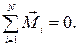 (2.27)
(2.27)
Поиск по сайту: