Кiнетична енергiя

Кiнетичною енергією 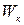називається енергiя тiла, що рухається. Визначимо кiнетичну енергiю тiла при поступальному русi. Нехай пiд дiєю сили 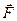тiло (матерiальна точка) масою m перемiстилося на 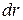, змiнивши при цьому свою швидкiсть на 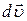. Тодi кiнетична енергiя тiла змiнилася на . Зрозумiло, що ця змiна кiнетичної енергiї вiдбулася за рахунок виконання силою 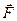роботи 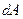(вважаємо, що сил опору та тертя немає):

,

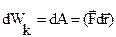Скористаємося виразом для елементарної роботи (2.49), другим законом Ньютона (2.8) та виразом для тангенцiального прискорення (1.25):

,

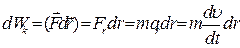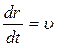Оскільки , а , то .

Якщо тiло починає рухатись iз стану спокою, тобто змінює свою швидкість вiд 0 до υ, воно набуде кiнетичну енергiю

.

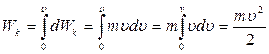Отже, кiнетична енергiя тiла (матерiальної точки) при поступальному русi дорiвнює:

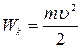(2.63)

Враховуючи, що iмпульс р = mυ, вираз (2.63) можна записати iнакше, помноживши i поділивши праву частину на m:

. (2.64)

Кінетична енергiя системи тiл (матерiальних точок) дорiвнює сумi кiнетичних енергiй окремих елементiв системи тобто є величиною адитивною.

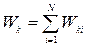(2.65)

Кiнетична енергiя є величиною вiдносною, i, як i швидкість, залежить вiд системи вiдлiку.

Знайдемо вираз для кiнетичної енергії АТТ, що обертається, як уже робилося ранiше, роздiлемо умовно АТТ на малi елементи m_i, для кожного з яких кiнетична енергiя за формулою (2.63) дорiвнюватиме

.

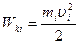Враховуючи вираз (2.65), а також рiвняння (1.60), запишемо для всього АТТ:

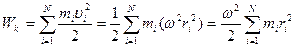
Оскільки 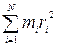є моментом iнерції I всього тiла, остаточно будемо мати для кiнетичної енергії обертального руху АТТ

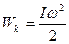(2.66)

Якщо швидкiсть тiла пiд дiєю сили 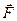змiнюється при поступальному русi вiд 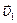до 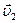то виконана при цьому робота сили дорiвнює змiнi кiнетичної енергiї тiла:

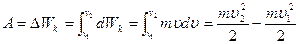(2.67)

Аналогiчне вiдбувається при обертальному русi, коли кутова швидкiсть АТТ змiнюється вiд 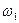до :

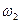(2.68)

Зрозумiло, що додатня робота приводить до збiльшення кiнетичної енергiї тiла, а вiд’ємна робота — до зменшення кiнетичної енергiї

Поиск по сайту: