 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Оценка ДП с неравными поступлениями
2.1 ОЦЕНКА ПОТОКА ПОСТНУМЕРАНДО
Прямая задачапредполагает оценку с позиции будущего, т.е. на конец периода п, когда реализуется схема наращения, которую можно представить следующим образом (рис. 7.6).
Таким образом, на первое денежное поступление С1 начисляются сложные проценты за (n - 1) период, и оно в конце n-гопериода станет равным C1(l + r)n-1. На второе денежное поступление С2 начисляются сложные проценты за (n-2)периода, и оно станет равным С2(1 + r)n-2и т.д. На предпоследнее денежное поступление Сn-1 проценты начисляются за один период, и оно будет в конце n-го периода равно Сn-1(1 + r).Естественно, на Сn проценты не начисляются.

Рис. 2. Логика решения прямой задачи для потока постнумерандо
Следовательно, наращенный денежный поток для исходного потока постнумерандо имеет вид:
C1 (1 + r)n-1, C2 (1 + r)n-2, …, Сn-1 (1 + r), Сn ,
и будущая стоимость FVpstисходного денежного потока (аннуитета) постнумерандо может быть оценена как сумма наращенных поступлений, т.е. получаем формулу:
FVpst = 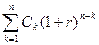 .
.
Обратная задача подразумевает оценку с позиции текущего момента, т.е. на конец периода 0. В этом случае реализуется схема дисконтирования, а расчеты необходимо вести по приведенному потоку. Элементы приведенного денежного потока уже можно суммировать; их сумма характеризует приведенную, или текущую, стоимость денежного потока, которую при необходимости можно сравнивать с величиной первоначальной инвестиции. Схема дисконтирования для исходного потока постнумерандо имеет следующий вид (рис. 3).
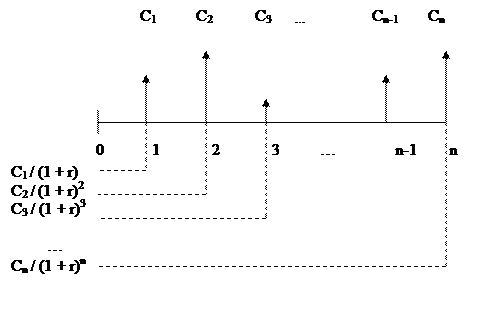
Рис. 3 Логика решения обратной задачи для потока постнумерандо
Таким образом, приведенный денежный поток для исходного потока постнумерандо имеет вид:
 ,
,  , …,
, …,  .
.
Приведенная стоимость денежного потока постнумерандо PVpstв общем случае может быть рассчитана по формуле:
PVpst = 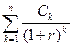 .
.
Если использовать дисконтирующий множитель, то формулу (7.16) можно переписать в следующем виде:
PVpst = 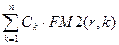 .
.
Пример
Рассчитать приведенную стоимость денежного потока постнумерандо (тыс. руб.): 12, 15, 9, 25, если ставка дисконтирования r = 12%.
| Год | Денежный поток (тыс. руб.) | Дисконтирующий множитель при r = 12% | Приведенный поток (тыс. руб.) |
| 0,8929 | 10,71 | ||
| 0,7972 | 11,96 | ||
| 0,7118 | 6,41 | ||
| 0,6355 | 15,89 | ||
| 44,97 |
 2..2 ОЦЕНКА ПОТОКА ПРЕНУМЕРАНДО
2..2 ОЦЕНКА ПОТОКА ПРЕНУМЕРАНДО
Логика оценки денежного потока в этом случае аналогична вышеописанной; некоторое расхождение в вычислительных формулах объясняется сдвигом элементов потока к началу соответствующих подынтервалов. Для прямой задачи схема наращения будет выглядеть следующим образом (рис. 4).

Рис. 4.Логика решения прямой задачи для потока пренумерандо
Следовательно, будущая стоимость исходного денежного потока пренумерандо FVpre в общем виде может быть рассчитана по формуле:
FVpre = 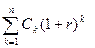
Очевидно, что FVpre = FVpsl · (1 + r).
Для обратной задачи схема дисконтирования может быть представлена следующим образом (рис. 5).
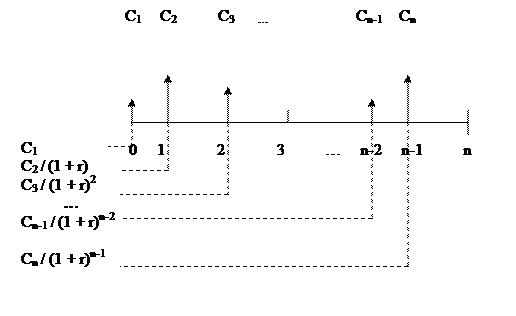
Рис. 5.Логика решения обратной задачи для потока пренумерандо
Таким образом, приведенный денежный поток для исходного потока пренумерандо имеет вид:
С1 , 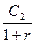 ,
, 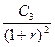 , …,
, …, 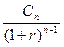
Следовательно, приведенная стоимость потока пренумерандо PVpre в общем виде может быть рассчитана по формуле:
PVpre = 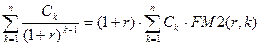 .
.
Как и в случае с будущей стоимостью, очевидно, что PVpre = PVpst × (1 + r).
Так, если в предыдущей задаче предположить, что исходный поток представляет собой поток пренумерандо, то его приведенная стоимость будет равна:
PVpre = PVpst · (1 + r) = 44,97 · 1,12 = 50,37 тыс. руб.
Поиск по сайту: