 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
ТЕМА 14. РИСК И ДОХОДНОСТЬ ИНВЕСТИЦИОННОГО ПОРТФЕЛЯ
В качестве численного показателя портфельного риска используются следующие показатели:
- ожидаемая доходность портфеля;
- стандартное отклонение портфеля;
- коэффициент вариации портфеля.
Ожидаемая доходность портфеля ценных бумаг это средневзвешенное значение ожидаемых доходностей отдельных активов, входящих в портфель; при этом их веса - это доли общей суммы инвестиций в портфель (часть всего портфеля) вложенные в соответствующие активы:
= 
* 
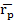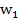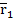+ w2 * 
+….+ 
* 
= 
,
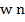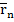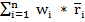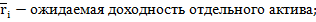
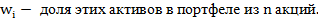
Ковариация (covariance) - это показатель, учитывающий как изменчивость (волатилъностъ) доходности акций или портфелей, так и тенденцию их доходности к росту или снижению по мере того, как растет или снижается доходность других акций или портфелей. Формула определяет ковариацию доходности активов А и В (Cov(AB)):
Cov (AB) = 
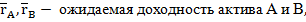
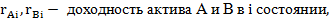
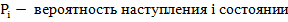
Величину ковариации обычно оказывается довольно сложно интерпретировать, и поэтому для измерения степени совместного изменения переменных чаще используется другой показатель - коэффициент корреляции (correlation coefficient). Коэффициент корреляции стандартизует ковариантность при делении на произведение, что облегчает сравнения при применении аналогичной шкалы. Коэффициент корреляции (rАВ) вычисляется для переменных следующим образом:
,
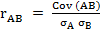Для определения риска портфеля, состоящего из двух активов, используют стандартное отклонение портфеля (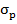
), которое рассчитывают по следующей формуле:
,
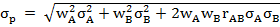Коэффициента вариаций портфеля ( VarАВ) рассчитывается как отношение стандартного отклонения портфеля к ожидаемой доходности портфеля:
Из нескольких альтернативных портфелей активов, предпочтение отдается тому портфелю, который имеет наименьший коэффициент вариации, т.е. имеет наименьший уровень риска на единицу доходности.
Задача. На основе данных рассчитать показатели риска портфеля № 1, состоящего из 50 % акций А и 50 % акций В, и портфеля № 2, состоящего из 30 % актива А и 70 % актива В. Какой портфель является наиболее предпочтительнее с точки зрения оптимизации риска и доходности?
Таблица – Вероятностные распределения доходности акций А и В.
| спрос | вероятность | Доходность акций, % | |
| А | В | ||
| Высокий | 0,3 | ||
| Средний | 0,4 | ||
| Низкий | 0,3 | -70 |
Решение:
1) На первом этапе рассчитываем ожидаемую доходность портфелей активов № 1 и 2, используя формулу:
0,5*15+0,5*15=15
0,3*15+0,7*15=15
На втором этапе рассчитываем стандартное отклонение портфелей № 1 и 2. Для этого необходимо рассчитать ковариацию, корреляцию:
Cov(AB) =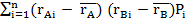 
Cov(AB) =(100-15)(20-15)*0,3+(15-15)(15-15)*0,4+(-70-15)(10-15)*0.3=255 255
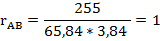
Значение коэффициента корреляции говорит о том, что связь между доходностями прямая.
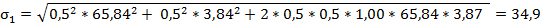
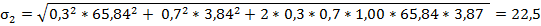
Первый портфель обладает более высоким риском по сравнению со вторым. Это происходит в результате того, что в первом портфеле удельный вес высокорискового актива «А» составляет 50%, в портфеле №2 - 30%
Далее рассчитаем коэффициент вариации:
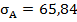
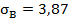
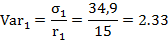
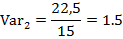
Вывод: Наиболее предпочтительным является второй портфель, т.к. он имеет коэффициент вариации.
Поиск по сайту: