 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Задача 1. 1.Функція F (х) називається первісною від функції f (х) на відрізку [a,b], якщо в усіх точках відрізку виконується рівність F ' (х) = f (х)
1. Функція F (х) називається первісною від функції f (х) на відрізку [ a, b ], якщо в усіх точках відрізку виконується рівність F ' (х) = f (х).
2. Множина усіх первісних F (х) + С для функції f (х) на відрізку [ a, b ] називається невизначеним інтегралом від f (х) і позначається  :
:
 .
.
Функція f (х) називається підінтегральною функцією, вираз f (х) dx – підінтегральним виразом, х – змінною інтегрування,  – знаком невизначеного інтеграла.
– знаком невизначеного інтеграла.
3. Таблиця основних невизначених інтегралів.
1.  . 9.
. 9.  .
.
2.  . 10.
. 10. 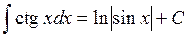 .
.
3. 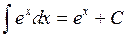 . 11.
. 11.  .
.
4.  . 12.
. 12.  .
.
5.  . 13.
. 13.  .
.
6. 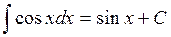 . 14.
. 14.  .
.
7.  . 15.
. 15.  .
.
8.  . 16.
. 16.  .
.
4. Властивості невизначеного інтеграла.
1. Похідна невизначеного інтеграла дорівнює підінтегральній функції:
 .
.
2. Постійний множник можна виносити за знак інтеграла:
 .
.
3. Невизначений інтеграл від алгебраїчної суми скінченого числа функцій дорівнює алгебраїчній сумі інтегралів від функцій, що додаються:
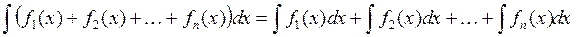 .
.
4. Якщо  ,то
,то  , де и = u (x) – довільна функція, яка має неперервну похідну.
, де и = u (x) – довільна функція, яка має неперервну похідну.
Поиск по сайту: