 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Задача 2. 1.Розглянемо функцію двох змінних z = f (х, у)
1. Розглянемо функцію двох змінних z = f (х, у). Позначимо приріст функції по змінній х при фіксованому значенні у, як Δх z = f (х + Δ х, у) – f (х, у), де Δ х – приріст х. Аналогічно, Δ уz = f (х, у + Δ у) – f (х, у), де Δ у – приріст у.
2. Частинною похідною по х від функції z = f (х, у) називається границя відношення приросту функції по х Δ хz до приросту змінної х, якщо останній прямує до нуля:
.
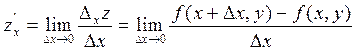3. Частинна похідна від функції z = f (х, у) по у визначається аналогічно:
.
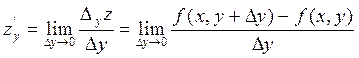4. Частинну похідну по х позначають: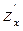 
, 
, 
, 
, 
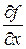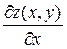. Частинну похідну по у можна позначити 
, 
, 
, 
, 
.
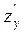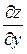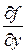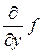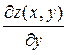5. При обчисленні похідної по змінній у постійною вважається х. Саме обчислення здійснюється за тими ж правилами і формулами, що і у функції однієї
змінної (див. частину 1 даних вказівок).
6. Щоб довести дану в задачі рівність треба обчислити частинні похідні від функції z = f (х, у). Потім підставити знайдені похідні в рівняння і виконати всі можливі тотожні перетворення. В результаті маємо отримати вірну рівність.
Поиск по сайту: