Задача 1. 1.Числовим рядом називається символ

1. Числовим рядом називається символ

,

де числа а ₁, а ₂, а ₃,… називаються членами ряду, член а_n – загальним членом ряда.

2. Сума n перших членів ряду називається n -ою частинною сумою ряду і позначається

.

3. Числовий рядназивається збіжним, якщо існує скінчена границя послідовності його частинних сум :

.

Число S називається сумою ряду. Якщо така границя не існує або дорівнює нескінченності, то ряд називається розбіжним.

4. Необхідна умова збіжності ряду. Якщо числовий ряд збігається, то загальний член ряду прямує до нуля при n → ∞:

.

Дана умова є тільки необхідною, але не достатньою для збіжності ряду. Якщо , то ряд розбігається. Якщо ж , то ряд може як збігатися, так і розбігатися.

5. Якщо при всіх n виконується нерівність а_n ≥ 0, то він називається рядом з невід’ємними членами. Якщо а_n > 0 при всіх n, то маємо ряд з додатними членами.

6. Ознака Даламбера.

Нехай ряд – ряд з додатними членами і існує скінчена границя

.

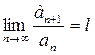Тоді, при l > 1 ряд розбігається, при l < 1 ряд збігається, при l = 1 треба досліджувати ряд за допомогою інших ознак.

7. Ознаку Даламбера зручно використовувати, коли загальний член ряду містить факторіали, показникові функції.

Поиск по сайту: