АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Задача 4. 1.Рівняннявигляду y'' + а1y' + а2y = 0, де – числа, y(x) – невідома функція, називається лінійним однорідним диференціальним рівнянням другого порядку зі

Читайте также:
  1. VI. Общая задача чистого разума
  2. В задачах 13.1-13.20 даны выборки из некоторых генеральных совокупностей. Требуется для рассматриваемого признака
  3. ВАША ЗАДАЧА
  4. Вопрос 2 Проверка и оценка в задачах со случайными процессами на примере решения задач экозащиты, безопасности и риска.
  5. Вот дела не задача
  6. Глава 10 Системный подход к задачам управления. Управленческие решения
  7. ГЛАВА 2.1. ЗАЩИТА ИННОВАЦИЙ КАК ЗАДАЧА УПРАВЛЕНИЯ ИННОВАЦИОННЫМИ ПРОЦЕССАМИ
  8. Глава 4. Математические основы оптимального управления в экономических задачах массового обслуживания
  9. Двойственная задача линейного программирования.
  10. Доклад о задачах власти Советов
  11. Доклад об экономическом положении рабочих Петрограда и задачах рабочего класса на заседании рабочей секции Петроградского совета рабочих и солдатских депутатов
  12. Задание 48: (Кейс 2 подзадача 1)

1. Рівняннявигляду y '' + а 1 y ' + а 2 y = 0, де – числа, y(x) – невідома функція, називається лінійним однорідним диференціальним рівнянням другого порядку зі сталими коефіцієнтами (ЛОДР ІІ).

2. Загальний розв’язок ЛОДР ІІ має вигляд:

узо = С 1 у 1 + С 2 у 2,

де - довільні сталі,

- два будь-які лінійно незалежні розв’язки ЛОДР ІІ. Ці розв’язки утворюють так звану фундаментальну систему розв’язків (ф. с. р.).

3. Розв’язок ЛОДР ІІ шукають у вигляді у = еkx. Тоді у ' = kеkx, у '' = k 2 еkx. Підставивши похідні в ЛОДР ІІ і скоротивши на еkx, отримаємо рівняння:

k 2 + а 1 k + а 2 = 0.

Таке рівняння є характеристичним рівнянням для ЛОДР ІІ. В залежності від його коренів ф.с.р. і загальний розв’язок ЛОДР ІІ приймають один з наступних виглядів.

4. Нехай характеристичне рівняння має два різних дійсних кореня k 1 ≠ k 2. Тоді , . Загальний розв'язок ЛОДР ІІ:

узо = С 1 + С 2 , С 1, С 2 R.

5. Нехай характеристичне рівняння має два однакових дійсних кореня k 1= k 2= k. Тоді , а в якості другого розв'язку беремо . Загальний розв'язок ЛОДР ІІ:

у зо = еkx (С 1 + С 2 х), С 1, С 2 R.

6. Нехай характеристичне рівняння має два комплексних спряжених кореня k 1,2 = α ± βі. Тоді ф. с. р. утворюють функці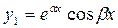ї і , а загальний розв'язок ЛОДР ІІ має вигляд:

у зо = е α x (С 1 + С 2 ), С 1, С 2 R.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)