Задача 5. 1.Якщо задана функція z = f (х; у) і напрямок , то границя відношення приросту функції Δf до Δρ при Δρ → 0 називається

1. Якщо задана функція z = f (х; у) і напрямок 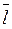, то границя відношення приросту функції Δ f до Δ ρ при Δ ρ → 0 називається похідною функції за напрямком 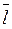і позначається

,

де , Δ х, Δ у – приріст аргументів х та у відповідно вздовж напрямку .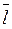

2. Величина похідної за напрямком 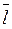визначає швидкість зміни функції в цьому напрямку. Знак похідної – характер зміни. Якщо > 0, то функція зростає у напрямку 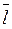, якщо < 0, то функція спадає за цим напрямком.

3. Якщо функція f (х; у) диференційована, то її похідна за довільним напрямком 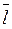існує і дорівнює

,

де 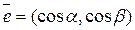– орт напрямку .

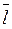4. Щоб знайти похідну функції z = f (х; у) за напрямком вектора треба:

– знайти частинні похідні функції;

– знайти напрямні косинуси вектора ;

– скористатися формулою для обчислення похідної за напрямом.

5. Щоб знайти похідну функції z = f (х; у) в точці М за напрямом даного вектора , треба підставити координати точки у вираз, що одержано в п. 4.

.

Поиск по сайту: