АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Задача 1. 1.Рівняння, які зв’язують невідому функцію, її диференціали або похідні та аргумент, називаються диференціальними (ДР)

Читайте также:
  1. VI. Общая задача чистого разума
  2. В задачах 13.1-13.20 даны выборки из некоторых генеральных совокупностей. Требуется для рассматриваемого признака
  3. ВАША ЗАДАЧА
  4. Вопрос 2 Проверка и оценка в задачах со случайными процессами на примере решения задач экозащиты, безопасности и риска.
  5. Вот дела не задача
  6. Глава 10 Системный подход к задачам управления. Управленческие решения
  7. ГЛАВА 2.1. ЗАЩИТА ИННОВАЦИЙ КАК ЗАДАЧА УПРАВЛЕНИЯ ИННОВАЦИОННЫМИ ПРОЦЕССАМИ
  8. Глава 4. Математические основы оптимального управления в экономических задачах массового обслуживания
  9. Двойственная задача линейного программирования.
  10. Доклад о задачах власти Советов
  11. Доклад об экономическом положении рабочих Петрограда и задачах рабочего класса на заседании рабочей секции Петроградского совета рабочих и солдатских депутатов
  12. Задание 48: (Кейс 2 подзадача 1)

1. Рівняння, які зв’язують невідому функцію, її диференціали або похідні та аргумент, називаються диференціальними (ДР). Коли невідома функція залежить лише від одного аргументу, тоді ДР називається звичайним.

2. Найвищий порядок похідної, що входить в ДР, називається порядком ДР.

3. Рівняння, яке пов’язує незалежну змінну х, невідому функцію у (х) та її похідну y ', називається ДР першого порядку:

F (x, y, y ') = 0 або y ' = f (х, у).

4. Розв’язком ДР першого порядку називається будь-яка функція у = φ (х), яка при підстановці її разом з похідною в рівняння, перетворює його в тотожність. Графік функції у = φ (х) називається інтегральною кривою.

5. Розв’язок ДР, який задовольняє початковій умові у (х 0) = у 0 , називається частинним розв’язком.

7. Задачу пошуку розв’язку ДР першого порядку, який задовольняє даній початковій умові, називають задачею Коші:

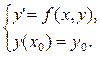– задача Коші.

8. Загальним розв’язком ДР першого порядку називається така функція у = φ (х, С), де С – довільна стала, що:

1. при будь-якому значенні С вона є розв’язком цього рівняння;

2. для будь-якої припустимої початкової умови у (х 0) = у 0 знайдеться таке значення сталої С = С 0, що φ (х 0, С 0) = у 0.

9. ДР вигляду M 1(х) N 1(у) dx + M 2(х) N 2(у) dy = 0 (або y ' = f 1(х) f 2(у)) називається рівнянням з відокремлюваними змінними. Щоб розв’язати таке рівняння, необхідно поділити обидві його частини на множник N 1(у) M 2(х) ≠ 0 (або на f 2 (у) ≠ 0), а потім проінтегрувати отримане рівняння. В результаті знайдемо загальний розв’язок рівняння.

10. Для знаходження частинного розв’язку слід замість х і у підставити в загальний розв’язок значення 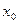і 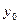відповідно. Отримаємо конкретне числове значення довільної сталої С. Підставивши це значення в загальний розв’язок рівняння, записуємо його частинний розв’язок.

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.004 сек.)