АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Задача 1. 1.Рівнянням 2-го порядку називається рівняння, що пов’язує незалежну змінну,невідому функцію і її перші дві похідні:

Читайте также:
  1. VI. Общая задача чистого разума
  2. В задачах 13.1-13.20 даны выборки из некоторых генеральных совокупностей. Требуется для рассматриваемого признака
  3. ВАША ЗАДАЧА
  4. Вопрос 2 Проверка и оценка в задачах со случайными процессами на примере решения задач экозащиты, безопасности и риска.
  5. Вот дела не задача
  6. Глава 10 Системный подход к задачам управления. Управленческие решения
  7. ГЛАВА 2.1. ЗАЩИТА ИННОВАЦИЙ КАК ЗАДАЧА УПРАВЛЕНИЯ ИННОВАЦИОННЫМИ ПРОЦЕССАМИ
  8. Глава 4. Математические основы оптимального управления в экономических задачах массового обслуживания
  9. Двойственная задача линейного программирования.
  10. Доклад о задачах власти Советов
  11. Доклад об экономическом положении рабочих Петрограда и задачах рабочего класса на заседании рабочей секции Петроградского совета рабочих и солдатских депутатов
  12. Задание 48: (Кейс 2 подзадача 1)

1. Рівнянням 2-го порядку називається рівняння, що пов’язує незалежну змінну,невідому функцію і її перші дві похідні:

F (x, y, у /, у //) = 0.

В багатьох випадках можна розв’язати це рівняння відносно старшої похідної:

y // = f (x, y, y).

2. Задача знаходження такого розв’язку рівняння, що задовольняє початковим умовам у (х 0) = у 0, у ' (х 0) = у 1 називається задачею Коші.

3. Загальним розв’язком рівняння другого порядку називається функція у = φ (х, С 1, С2) така, що:

1. при будь-яких довільних сталих С 1, С2 перетворює дане рівняння в тотожність;

2. при будь-яких початкових умовах знайдуться такі значення довільних сталих С 1*, С2 *, при яких φ (х 0, С 1*, С2 *) = у 0.

4. Будь-яка функція у = φ (х, С 10, С2 0), яка отримана із загального розв’язку при конкретних значеннях сталих С 1, С2 називається частинним розв’язком.

5. Дане рівняння, не містить явно шукану функцію у(х): F (x, y ', y)=0. Можна знизити порядок рівняння підстановкою у ' = р (х), у '' = р ' (х), де р (х) – нова невідома функція.

6. Підставивши вирази у ' = р (х), у '' = р ' (х) в дане рівняння, після спрощень отримаємо диференціальне рівняння першого порядку відносно функції р (х) (див. частину ІV).

7. Розв’язавши отримане рівняння, знайдемо функцію р (х). Робимо зворотну підстановку у ' = р (х). Отримаємо диференціальне рівняння першого порядку відносно функції у(х). Розв’язавши це рівняння, отримаємо загальний розв’язок даного диференціального рівняння другого порядку.

8. Для знаходження розв’язку задачі Коші знайдемо похідну 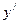. Потім підставимо в у і 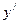замість х, у і 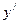значення 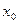, 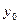і відповідно. Виконавши обчислення, отримаємо систему лінійних алгебраїчних рівнянь для знаходження невідомих коефіцієнтів .

9. Розв’язавши систему з п.8, підставимо знайдені значення коефіцієнтів 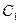і в у(х). Отриманий розв’язок є частинним розв’язком даного диференціального рівняння.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)