АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Задача 2. 1.Ряд, що містить і додатні і від’ємні члени називається знакозмінним

Читайте также:
  1. VI. Общая задача чистого разума
  2. В задачах 13.1-13.20 даны выборки из некоторых генеральных совокупностей. Требуется для рассматриваемого признака
  3. ВАША ЗАДАЧА
  4. Вопрос 2 Проверка и оценка в задачах со случайными процессами на примере решения задач экозащиты, безопасности и риска.
  5. Вот дела не задача
  6. Глава 10 Системный подход к задачам управления. Управленческие решения
  7. ГЛАВА 2.1. ЗАЩИТА ИННОВАЦИЙ КАК ЗАДАЧА УПРАВЛЕНИЯ ИННОВАЦИОННЫМИ ПРОЦЕССАМИ
  8. Глава 4. Математические основы оптимального управления в экономических задачах массового обслуживания
  9. Двойственная задача линейного программирования.
  10. Доклад о задачах власти Советов
  11. Доклад об экономическом положении рабочих Петрограда и задачах рабочего класса на заседании рабочей секции Петроградского совета рабочих и солдатских депутатов
  12. Задание 48: (Кейс 2 подзадача 1)

1. Ряд, що містить і додатні і від’ємні члени називається знакозмінним.

2. Частинним випадком знакозмінних рядів є знакопереміжні ряди.

Ряд, в якому будь-які два сусідні члени мають різні знаки, називаються знакопереміжними:

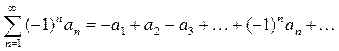
або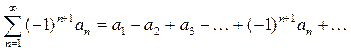

де а 1, а 2, …, аn, … – додатні дійсні числа.

3. Знакопереміжні ряди досліджують на збіжність за ознакою Лейбніца.

Нехай даний знакопереміжний ряд 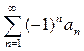або 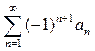. Якщо:

1) абсолютні величини членів ряду монотонно спадають (а 1 > а 2 > а 3>…) і

2) загальний член ряду прямує до нуля при n → ∞ (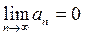), то ряд збігається.

4. Якщо хоча б одна з умов не виконується, то ряд розбігається.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.005 сек.)