АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Задача 3. 1.Ряд, членами якого є функції, називається функціональним:

Читайте также:
  1. VI. Общая задача чистого разума
  2. В задачах 13.1-13.20 даны выборки из некоторых генеральных совокупностей. Требуется для рассматриваемого признака
  3. ВАША ЗАДАЧА
  4. Вопрос 2 Проверка и оценка в задачах со случайными процессами на примере решения задач экозащиты, безопасности и риска.
  5. Вот дела не задача
  6. Глава 10 Системный подход к задачам управления. Управленческие решения
  7. ГЛАВА 2.1. ЗАЩИТА ИННОВАЦИЙ КАК ЗАДАЧА УПРАВЛЕНИЯ ИННОВАЦИОННЫМИ ПРОЦЕССАМИ
  8. Глава 4. Математические основы оптимального управления в экономических задачах массового обслуживания
  9. Двойственная задача линейного программирования.
  10. Доклад о задачах власти Советов
  11. Доклад об экономическом положении рабочих Петрограда и задачах рабочего класса на заседании рабочей секции Петроградского совета рабочих и солдатских депутатов
  12. Задание 48: (Кейс 2 подзадача 1)

1. Ряд, членами якого є функції, називається функціональним:

,

причому, всі функції повинні бути визначені і неперервні в одному інтервалі.

2. Якщо в функціональний ряд замість х підставити конкретне значення х = х 0, то він стане числовим. Для одних значень х ряд може збігатися, для інших – розбігатися.

3. Значення х = х 0, при яких числовий ряд збігається, називається точкою збіжності функціонального ряду. Множина всіх точок збіжності функціонального ряду називається областю його збіжності.

4. Частиннимвипадком функціонального ряду є степеневий ряд, тобто ряд вигляду ,

де а 0, а 1, …, аn, … числа, які називаються коефіцієнтами степеневого ряду.

5. При х 0 = 0 степеневий ряд має вигляд

6. Всі степеневі ряди збігаються при .

7. Для дослідження степеневого ряду на збіжність треба знайти радіус та інтервал збіжності.

8. Радіусом збіжності степеневого ряду називається таке число R, що для всіх х таких, що < R, ряд збігається абсолютно, а для всіх х таких, що > R, ряд розбігається.

9. Радіус збіжності степеневого ряду знаходиться за формулою:

.

10. Інтервалом збіжності степеневого ряду називається інтервал

(х 0 – R; х 0 + R).

11. Якщо степеневий ряд збігається при всіх х, то вважають, що R = ∞. Якщо ряд розбігається при всіх х, крім х = 0, то вважають R = 0.

12. На кінцях інтервалу збіжності (при і 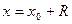) необхідно провести додаткове дослідження. Ряд може збігатися в обох точках, або тільки в одній з них, або розбігатися в обох. Для дослідження треба підставити значення і 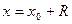в степеневий ряд і дослідити отриманий числовий ряд (див. задачі 1,2).


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)