АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Задача 3. 1. Точка М0 (x0; y0) називається точкою екстремуму (максимуму чи мінімуму) функції z = f (х; у), якщо f(x0; y0) є відповідно найбільше чи найменше значення

Читайте также:
  1. VI. Общая задача чистого разума
  2. В задачах 13.1-13.20 даны выборки из некоторых генеральных совокупностей. Требуется для рассматриваемого признака
  3. ВАША ЗАДАЧА
  4. Вопрос 2 Проверка и оценка в задачах со случайными процессами на примере решения задач экозащиты, безопасности и риска.
  5. Вот дела не задача
  6. Глава 10 Системный подход к задачам управления. Управленческие решения
  7. ГЛАВА 2.1. ЗАЩИТА ИННОВАЦИЙ КАК ЗАДАЧА УПРАВЛЕНИЯ ИННОВАЦИОННЫМИ ПРОЦЕССАМИ
  8. Глава 4. Математические основы оптимального управления в экономических задачах массового обслуживания
  9. Двойственная задача линейного программирования.
  10. Доклад о задачах власти Советов
  11. Доклад об экономическом положении рабочих Петрограда и задачах рабочего класса на заседании рабочей секции Петроградского совета рабочих и солдатских депутатов
  12. Задание 48: (Кейс 2 подзадача 1)

1. Точка М 0 (x 0; y 0) називається точкою екстремуму (максимуму чи мінімуму) функції z = f (х; у), якщо f (x 0; y 0) є відповідно найбільше чи найменше значення функції f (х; у) в деякому околі точки М 0 (x 0; y 0): f (x 0; y 0) > f (х; у) чи f (x 0; y 0) < < f (х; у) в усіх точках М (х; у) ≠ М 0 (x 0; y 0) з деякого околу точки М 0.

2. Значення f (x 0; y 0) називається максимальним (або мінімальним) значенням функції.

3. Необхідна умова екстремуму. Якщо в точці М 0 (x 0; y 0) диференційована функція z = f (х; у) має екстремум, то її частинні похідні в цій точці дорівнюють нулю:

і .

Точка М 0 (x 0; y 0), в якій обидві частинні похідні дорівнюють нулю, називається стаціонарною.

4. Якщо функція z = f (х, у) має частинні похідні і , то вони в загальному випадку також є функціями двох змінних. Частинні похідні від цих функцій називаються другими частинними похідними від функції z = f (х, у) і позначаються так:

, , , .

Похідні 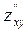та називаються мішаними.

5. Достатня умова екстремуму. Нехай точка М 0 (x 0; y 0) є стаціонарною точкою функції z = f (х; у). Позначимо

, , .

Якщо АС – В 2 > 0 і А < 0, то М 0 (x 0; y 0) – точка максимуму.

Якщо АС – В 2 > 0 і А > 0, то М 0 (x 0; y 0) – точка мінімуму.

Якщо АС – В 2 < 0, то М 0 (x 0; y 0) не є точкою екстремуму.

Якщо АС – В 2 = 0, то необхідне додаткове дослідження.

6. Щоб знайти екстремум функції двох змінних z = f (х; у) треба:

– знайти область визначення функції;

– знайти частинні похідні і прирівняти їх до нуля;

– скласти з отриманих рівнянь систему і розв’язати її; знайдені точки є стаціонарними;

– обчислити частинні похідні другого порядку від функції z = f (х; у);

– знайти значення А, В, С в кожній із стаціонарних точок;

– знайти величину АС – В 2 і зробити висновок;

– якщо в досліджуваній стаціонарній точці є екстремум, то підставити координати точки в функцію z = f (х; у). Знайдене значення буде максимальним (або мінімальним) значенням функції.

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)