 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Задача 3. 1.Якщо підінтегральний вираз можна записати у вигляді добутку udv, де u(x)
1. Якщо підінтегральний вираз можна записати у вигляді добутку udv, де u(x)
i v(x) – функції, які мають неперервні похідні, то має місце формула інтегрування частинами:
.
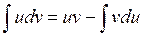2. Записати підінтегральний вираз у вигляді добутку udv можна декількома способами. Причому, множник dv обов’язково містить диференціал змінної інтегрування. Після вибору множників u і dv треба диференціюванням знайти du та інтегруванням – v. При обчисленні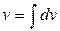 
довільну сталу опускають. Отримані значення u, v та du підставляють в праву частину формули. Множники u і dv будуть вибрані вірно, якщо інтеграл 
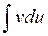є простішим за інтеграл 
.
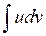Розглянемо основні типи інтегралів, які легко обчислити інтегруванням частинами.
3. В інтегралах вигляду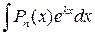 
, 
, 
, 
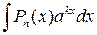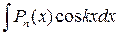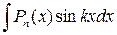, де Рn (х) – многочлен n -го степеня, k – число, зручно вибрати множник u = Рn (х), dv – всі інші множники.
4. В інтегралах вигляду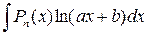 
зручно взяти dv = Рn (х) dх, а u =ln(ах + b).
5. В інтегралах вигляду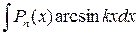 
, 
, 
, 
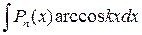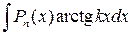, де Рn (х) – многочлен, k – число, вибирають dv = Рn (х) dх, за u – функцію, що є множником при Рn (х).
6. Метод інтегрування частинами можна, у разі необхідності, застосовувати декілька разів поспіль або комбінуючи з іншими методами інтегрування.
Поиск по сайту: