Задача 5. 1.Лінійні неоднорідні диференціальні рівняння другого порядку зі сталими коефіцієнтами (ЛНДР ІІ) – це рівняння вигляду y'' + а1y' + а2y = f (x)

1. Лінійні неоднорідні диференціальні рівняння другого порядку зі сталими коефіцієнтами (ЛНДР ІІ) – це рівняння вигляду y '' + а ₁ y ' + а ₂ y = f (x), де f(x) – довільна неперервна функція.

2. Загальний розв'язок у_зн ЛНДР ІІ має вигляд

у_зн = у_зо + у_ч,

де у_зо – загальний розв'язок відповідного однорідного рівняння,

у_ч – деякий частинний розв'язок даного неоднорідного рівняння.

3. Для розв’язання ЛНДР ІІ необхідно спочатку знайти загальний розв’язок відповідного однорідного рівняння (див. задачу 4).

4. Якщо права частина рівняння f(x) має спеціальний вигляд, то частинний розв’язок у_ч шукаємо методом невизначених коефіцієнтів.

5. Деякі спеціальні праві частини і відповідні їм частинні розв’язки рівняння наведені в наступній таблиці:

	f (x) = еаxРn (х)	уч = , де S = 0, якщо k 1 ≠ а і k 2 ≠ а, S = 1, якщо k 1 = а або k 2 = а, S = 2, якщо k 1 = k 2 = а; Qn (х) – многочлен степеня n з невизначеними коефіцієнтами.
	f (x) =	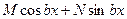уч = , де S = 1, якщо k 1,2 = ± bi, S = 0 в інших випадках; А, В – невизначені коефіцієнти.

6. Для знаходження розв’язку у_ч треба вибрати відповідний вигляд розв’язку з таблиці, знайти похідні і підставити у_ч, в неоднорідне рівняння. Спростити отримане рівняння, скласти систему для знаходження невідомих коефіцієнтів і розв’язати її. Для складання системи необхідно прирівняти коефіцієнти при однакових степенях х в обох частинах рівняння (випадок 1) або при однакових тригонометричних функціях (випадок 2).

7. Визначені в п.6коефіцієнти підставимо в частинний розв’язок у_ч. Загальний розв’язок 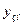ЛНДР ІІ отримаємо склавши розв’язки і у_ч.

Поиск по сайту: