Задача 5. 1.Позначимо R (sin x, cos x) функцію зі змінними sin x та cos x, над якими виконані дії додавання, віднімання

1. Позначимо R (sin x, cos x) функцію зі змінними sin x та cos x, над якими виконані дії додавання, віднімання, множення або ділення (R – знак раціональної функції).

2. Будь-який інтеграл виду можна за допомогою підстановки привести до інтеграла від функції, раціональної відносно t. В цьому випадку , , , а

.

Така підстановка називається універсальною тригонометричною підстановкою.

В ряді випадків при інтегруванні тригонометричних функцій можна скористатися більш простими підстановками. Зокрема, однією з наступних, в залежності від вигляду підінтегральної функції.

3. В інтегралах , де R – раціональна функція, можна застосувати підстановку t = sin х; в інтегралах вигляду – підстановку t = cos х.

4. Коли інтеграл має вигляд , де R – раціональна функція, то він спрощується за допомогою підстановки tg x = t.

5. Інтеграл вигляду спрощується заміною змінних, яку зручно обрати в залежності від значень m і n, а саме:

5.1. коли n – ціле додатне непарне число, такий інтеграл можна спростити підстановкою t = sin х;

5.2. підстановку t = cos х використовують, коли m – ціле додатне непарне число;

5.3. якщо m і n – цілі невід’ємні парні числа, то для спрощення інтеграла можна застосувати формули зниження степеня тригонометричних функцій:

, ;

5.4. коли (m + n) – ціле від’ємне парне число, то використовують підстановку tg x = t.

6. Інтеграли вигляду , , 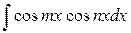обчислюються за допомогою формул:

,

,

.

Поиск по сайту: