Замечания. 1. Аналогичные определения глобального максимума и локального максимума можно получить путем замены знака неравенства на противоположный

1. Аналогичные определения глобального максимума и локального максимума можно получить путем замены знака неравенства на противоположный.

2. Если функция обладает свойством унимодальности, то локальный минимум автоматически является глобальным минимумом.

Рис. 2.7. Локальные и глобальные оптимумы.

3. Если функция не является унимодальной, то возможно нали­чие нескольких локальных оптимумов; при этом глобальный минимум можно определить путем нахождения всех локальных оптимумов и выбора наименьшего из них.

На рис. 2.7 точка 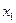— точка глобального максимума, 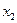— точка локального минимума, — точка локального максимума, — точка глобального минимума, а Хь можно рассматривать и как точку локального минимума, и как точку локального максимума.

Идентификация оптимумов в случае функции одной переменной.

Предположим, что функция f (х) одной переменной х определена на открытом интервале (а, b) и n -кратно дифференцируема на этом интервале. Если х* — внутренняя точка интервала, то теорема Тейлора позволяет записать изменение функции f при переходе от точки х* к точке () в следующем виде:

где через 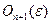обозначена сумма членов, в которых степень 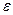равна (n+1) и выше. Если х*— локальный минимум функции f на (а, b), то по определению должна существовать 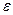-окрестность точки x*, такая, что для всех х из этой окрестности выполняется неравенство

Из неравенства (2.2) следует, что

При достаточно малом 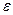первое слагаемое доминирует над осталь­ными, а так как 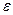можно выбрать и положительным, и отрицательным, то неравенство (2.3) будет выполняться только в том случае, если

Рассуждая аналогичным образом, нетрудно установить, что неравенство (2.3) будет справедливым только тогда, когда

Эта же схема анализа применима и в случае локального максимума, с той лишь разницей, что знак неравенства (2.2) требуется заменить на противоположный. Мы получили следующий общий результат, который можно сформулировать в виде теоремы.

Теорема 2.1

Необходимые условия того, что х* является точкой локального минимума (максимума) дважды дифференцируемой функции f на открытом интервале (а, b), выражаются следующими соотношениями:

.

Эти условия являются необходимыми, т. е. в случае, когда они не выполняются, точка х* не может быть точкой локального минимума (максимума). С другой стороны, если эти условия выполня­ются, мы не имеем гарантии, что х* является точкой локального минимума (максимума). Рассмотрим, например, функцию 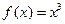, график которой представлен на рис. 2.8. Эта функция удовлетворяет необходимым условиям наличия, как локального минимума, так и локального максимума в начале коор­динат, однако не имеет ни максимума, ни минимума при х*=0.

Рис. 2.8. Точка перегиба.

Определения Стационарной точкой называется точка х*, в которой

.

Если стационарная точка не соответствует локальному оптимуму (минимуму или максимуму),то она является точкой перегиба, или седловой точкой.

Для того чтобы провести различие между случаями, когда стационарная точка соответствует локальному минимуму, локальному максимуму или является точкой перегиба, необходимо построить достаточные условия оптимальности.

Теорема 2.2

Пусть в точке первые (п— 1) производные функции обращаются в нуль, а производная порядка п отлична от нуля.

(1) Если п — нечетное, то х*— точка перегиба.

(2) Если п — четное, то х*— точка локального оптимума.

Кроме того,

(а) если эта производная положительная, то х*— точка локального минимума;

(б) если эта производная - отрицательная, то х* —точка локального максимума.

Доказательство

Утверждение теоремы нетрудно доказать с помощью разложения в ряд Тейлора, представленного равенством (2.1). Поскольку порядок первой отличной от нуля производной равен n, формулу (2.1) можно переписать в следующем виде:

Если п — нечетное число, то правая часть (2.6) может принимать как положительные, так и отрицательные значения в зависимости от того, является ли величина 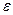положительной или отрицательной. Это означает, что в зависимости от знаки 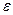разность f(x^-\-v)—f(x*) либо положительная, либо отрицательная. Следовательно, функция не достигает в точке х* своею минимального или максимального значения, т.е. х* — точка перегиба.

Далее рассмотрим случай, когда п — четное число. При этом величина всегда положительная, а знак правой части (2.6) определяется первым слагаемым, если 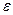— достаточно малая величина. Таким образом, если величина положительная, то и точка х* соответствует локальному минимуму. Аналогичные рассуждения нетрудно провести также и для локального максимума.

Для того чтобы применить теорему 2.2 к функции 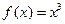, график которой изображен на рис. 2.8, вычислим

Так как порядок первой отличной от нуля производной равен 3 (нечетное число), точка х=0 является точкой перегиба.

Поиск по сайту: