АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Метод средней точки

Читайте также:
  1. A)нахождение средней из двух соседних средних, для отнесения полученного результата к определенной дате
  2. F. Метод, основанный на использовании свойства монотонности показательной функции .
  3. FAST (Методика быстрого анализа решения)
  4. I этап Подготовка к развитию грудобрюшного типа дыхания по традиционной методике
  5. I. 2.1. Графический метод решения задачи ЛП
  6. I. 3.2. Двойственный симплекс-метод.
  7. I. ГИМНАСТИКА, ЕЕ ЗАДАЧИ И МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ
  8. I. Метод рассмотрения остатков от деления.
  9. I. Методические основы
  10. I. Методические основы оценки эффективности инвестиционных проектов
  11. I. Организационно-методический раздел
  12. I. Предмет и метод теоретической экономики

Если функция f(x) унимодальна в заданном интервале поиска, то точкой оптимума является точка, в которой f'(х)=0. Если при этом имеется возможность вычислять как значения функции, так и се производной, то для нахождения корня уравнения можно воспользоваться эффективным алгоритмом исключения интервалов, на каждой итерации которого рассматривается лишь одна пробная точка. Например, если в точке z выполняется неравенство , то с учетом предположения об унимодальности естественно утверждать, что точка минимума не может находиться левее точки z. Другими словами, интервал подлежит исключению. С другой стороны, если , то точка минимума не может находиться правее z и интервал можно исключить. Приведенные рассуждения лежат в основе логической структуры метода средней точки, который иногда называют поиском Больцано.

Определим две точки L и R таким образом, 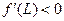и . Стационарная точка расположена между L и R. Вычислим значение производной функции в средней точке рассматриваемого интервала . Если , то интервал (z, R) можно исключить из интервала поиска. С другой стороны, если ,то можно исключить интервал (L, z). Ниже дается формализованное описание шагов алгоритма.

Пусть имеется ограниченный интервал и задан параметр сходимости .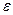

Шаг 1. Положить R=b, L=a при этом f'(а)<.0 и f'(b)>0.

Шаг 2. Вычислить и f'(z).

Шаг 3. Если , закончить поиск. В противном случае, если , положить L=z и перейти к шагу 2. Если положить R-=z и перейти к шагу 2.

Следует отметить, что логическая структура поиска в соответствии с изложенным методом исключения интервалов основана лишь на исследовании знака производной независимо от значений, которые эта производная принимает. В следующем подразделе рассматривается метод секущих [2], при реализации которого рассматриваются как знак производной, так и ее значения.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.004 сек.)