АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Методы с использованием производных

Читайте также:
  1. II. Методы непрямого остеосинтеза.
  2. II. Рыночные методы.
  3. III. Методы искусственной физико-химической детоксикации.
  4. III. Параметрические методы.
  5. III. Разведение спирта с использованием таблиц ГФ XI.
  6. III. Создание и обработка комплексного информационного объекта в виде презентации с использованием шаблонов.
  7. IV. Современные методы синтеза неорганических материалов с заданной структурой
  8. А. Механические методы
  9. Автоматизированные методы
  10. Автоматизированные методы анализа устной речи
  11. Адаптивные методы прогнозирования
  12. Административно-правовые методы государственного управления

Все рассмотренные в предыдущих разделах методы поиска основываются на предположениях об унимодальности и в ряде случаев о непрерывности исследуемой целевой функции. Целесообразно предположить, что если в дополнение к условию непрерывности ввести требование дифференцируемости функции, то эффективность поисковых процедур можно существенно повысить. Напомним, что в разд. 2.2 установлено необходимое условие существования локального минимума функции в некоторой точке z, согласно которому первая производная функции в точке z должна обращаться в нуль, т.е.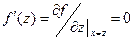

Если функция f(x) содержит члены, включающие х в третьей и более высоких степенях, то непосредственное получение аналитического решения уравнения может оказаться затруднительным. В таких случаях используются приближенные методы последовательного поиска стационарной точки функции . Прежде всего, опишем классическую поисковую схему, ориентированную на нахождение корня нелинейного уравнения. Эта схема была разработана Ньютоном и позднее уточнена Рафсоном [5].


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)