АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Этап установления границ интервала

Читайте также:
  1. II. 4.1. Алгоритм метода ветвей и границ
  2. II. Типичные структуры и границы
  3. II.4. МЕТОД ВЕТВЕЙ И ГРАНИЦ В ЗАДАЧАХ ЦЕЛОЧИСЛЕННОГО ПРОГРАММИРОВАНИЯ
  4. III Общий порядок перемещения товаров через таможенную границу Таможенного союза
  5. VII. СУЩЕСТВУЮТ ЛИ ГРАНИЦЫ ПОЗНАНИЯ?
  6. а) Находим границы, в которых с вероятностью 0,9946 заключено среднее время обслуживания всех клиентов пенсионного фонда.
  7. А) совокупность предусмотренных законодательством видов и ставок налога, принципов, форм и методов их установления.
  8. Адсорбция на границе газ-жидкость. Изотерма Гиббса.
  9. Адсорбция на границе «жидкость – газ»
  10. Алгоритм метода ветвей и границ
  11. Биосфера: понятие и современные представления, функции. Вклад Ж-Б Ламарка, Э. Зюсса, В.И. Вернадского. Эволюция биосферы. Границы биосферы.
  12. БІОСФЕРА І ЇЇ ГРАНИЦІ

На этом этапе сначала выбирается исходная точка, а затем на основе правила исключения строится относительно широкий интервал, содержащий точку оптимума. Обычно поиск граничных точек такого интервала проводится с помощью эвристических методов поиска, хотя в ряде случаев можно также использовать методы экстраполяции. В соответствии с одним из эвристических методов, который был предложен Свенном [I], (k+1)-я пробная точка определяется по рекуррентной формуле

где - произвольно выбранная начальная точка, — подбираемая некоторым способом величина шага. Знак определяется путем сравнения значений 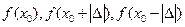. Если

то, согласно предположению об унимодальности, точка минимума должна располагаться правее точки и величина выбирается положительной. Если изменить знаки неравенств на противоположные,то следует выбирать отрицательной. Еслиже

то точка минимума лежит между и и поиск граничных точек завершен. Случай, когда

противоречит предположению об унимодальности. Выполнение этого условия свидетельствует о том, что функция не является унимодальной.

Пример 2.1

Установить границы интервала в задаче минимизации функции при заданной начальной точке =30 и величине шага =5.

Знак определяется на основе сравнения значений

Так как

то величина должна быть положительной, а координата точки минимума х* должна быть больше 30. Имеем 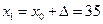. Далее , ,

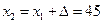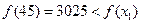откуда х*>35.

,

откуда х*>45.

,

откуда х*>65.

,

следовательно, х*<185. Таким образом, шесть шагов вычислений х* позволили выявить интервал , в котором расположена точка х*. Заметим, что эффективность поиска граничных точек непосредственно зависит от величины шага . Если велико, то получаем грубые оценки координат граничных точек, и построенный интервал оказывается весьма широким. С другой стороны, если мало, для определения граничных точек может потребоваться достаточно большой объем вычислений.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.007 сек.)