АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Метод последовательного оценивания с использованием квадратичной аппроксимации

Читайте также:
  1. F. Метод, основанный на использовании свойства монотонности показательной функции .
  2. FAST (Методика быстрого анализа решения)
  3. I этап Подготовка к развитию грудобрюшного типа дыхания по традиционной методике
  4. I. 2.1. Графический метод решения задачи ЛП
  5. I. 3.2. Двойственный симплекс-метод.
  6. I. ГИМНАСТИКА, ЕЕ ЗАДАЧИ И МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ
  7. I. Метод рассмотрения остатков от деления.
  8. I. Методические основы
  9. I. Методические основы оценки эффективности инвестиционных проектов
  10. I. Организационно-методический раздел
  11. I. Предмет и метод теоретической экономики
  12. I. Что изучает экономика. Предмет и метод экономики.

Этот метод, разработанный Пауэллом [4], основан на последовательном применении процедуры оценивания с использованием квадратичной аппроксимации. Схему алгоритма можно описать следующим образом. Пусть 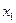- начальная точка, - выбранная величина шага по оси х.

Шаг 1. Вычислить .

Шаг 2. Вычислить и .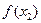

Шаг 3. Если , положить . Если , положить .

Шаг 4. Вычислить и найти

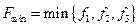
=точка , которая соответствует .

Шаг 5. По трем точкам вычислить , используя формулу для оценивания с помощью квадратичной аппроксимации.

Шаг 6. Проверка на окончание поиска.

(a) Является ли разность достаточно малой?

(б) Является ли разность достаточно малой?

Если оба условия выполняются, закончить поиск. В противном случае перейти к шагу 7.

Шаг 7. Выбрать «наилучшую» точку ( или ) две точки по обе стороны от нее. Обозначить эти точки в естественном порядке и перейти к шагу 4.

Заметим, что при первой реализации шага 5 границы интервала, содержащего точку минимума, не обязательно оказываются установленными. При этом полученная точка может находитьсязаточкой . Для того чтобы исключить возможность слишком большого экстраполяционного перемещения, следует провести после шага 5 дополнительную проверку и в случае, когда точка находится слишком далеко от , заменить точкой, координата которой вычисляется с учетом заранее установленной длины шага.

Пример 2.5

Минимизировать функцию , используя метод Пауэлла

Пусть начальная точка и длина шага . Для проверкинаокончание поиска используются следующие параметры сходимости:

Итерация 1

Шаг 1. .

Шаг 2. .

Шаг 3. , следовательно,положить .

Ш а г 4.

Шаг 5.

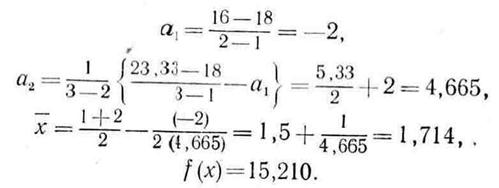
Ш а г 6. Проверка на окончание поиска:

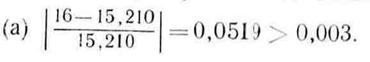
Следовательно, продолжаем поиск.

Шаг 7. Выбираем как «наилучшую» точку, a и - как точки, которые ее окружают. Обозначаем, эти точки в естественном порядке и переходим к итерации 2, которая начинается с шага 4.

Итерация 2

Ш а г 5.

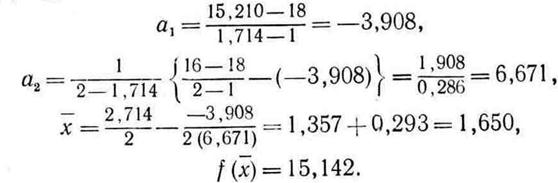
Ш а г 6. Проверка на окончание поиска:

(а) (условие не выполняется).

Шаг 7. Выбираем как «наилучшую» точку, a — как точки, которые ее окружают.

Итерация 3.

Шаг 4.

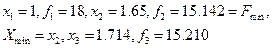
Шаг 5.

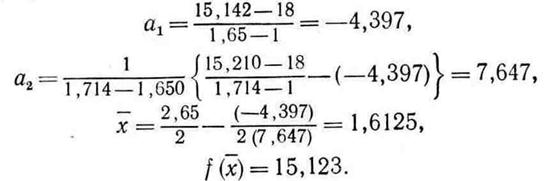
Шаг 6. Проверка на окончание поиска:

(а ,

(б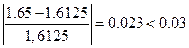

Следовательно, поиск закончен.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.004 сек.)