АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Метод деления интервала пополам

Читайте также:
  1. F. Метод, основанный на использовании свойства монотонности показательной функции .
  2. FAST (Методика быстрого анализа решения)
  3. FSBFRUL (Ф. Правило распределения ассигнований по КЭКР.Заголовки)
  4. I Определения
  5. I этап Подготовка к развитию грудобрюшного типа дыхания по традиционной методике
  6. I. 2.1. Графический метод решения задачи ЛП
  7. I. 3.2. Двойственный симплекс-метод.
  8. I. ГИМНАСТИКА, ЕЕ ЗАДАЧИ И МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ
  9. I. Дайте определения следующих правовых категорий.
  10. I. Метод рассмотрения остатков от деления.
  11. I. Методические основы
  12. I. Методические основы оценки эффективности инвестиционных проектов

Рассматриваемый метод позволяет исключать в точности половину интервала на каждой итерации. Иногда этот метод называют трехточечным поиском на равных интервалах, поскольку его реализация основана на выборе трех пробных точек, равномерно распределенных в интервале поиска. Ниже приводится описание основных шагов поисковой процедуры, ориентированных на нахождение точки минимума функции 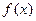в интервале (а,b).

Шаг 1. Положить и L=b—а. Вычислить значение .

Шаг 2. Положить, и . Заметим, что точки делят интервал (а, b) на четыре равные части. Вычислить значения и .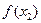

Шаг 3. Сравнить и .

(1) Если , исключить интервал (), положив .

Средней точкой нового интервала поиска становится точка 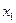. Следовательно, необходимо положить 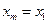. Перейти к шагу 5.

(2) Если , перейти к шагу 4.

Шаг 4. Сравнить 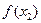и .

(1) Если исключить интервал (), положив . Так как средней точкой нового интервала становится точка 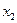положить . Перейти к шагу 5.

(2) Если 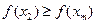, исключить интервалы () и ( ). Положить и . Заметим, что продолжает оставаться средней точкой нового интервала. Перейти к шагу 5.

Шаг 5. Вычислить . Если величина мала, закончить поиск. В противном случае вернуться к шагу 2.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)