Метод секущих (хорд)

Метод секущих, являющийся комбинацией метода Ньютона и общей схемы исключения интервалов, ориентирован на нахождение корня уравнения в интервале (а, b), если, разумеется, такой корень существует.

Рис. 2.15. Метод секущих

Предположим, что в процессе поиска стационарной точки функции f(x) в интервале (а, b) обнаружены две точки L и R, в которых знаки производной различны. В этом случае алгоритм метода секущих позволяет аппроксимировать функцию f'(x) «секущей прямой» (прямой линией, соединяющей две точки) и найти точку, в которой секущая графика f'(x) пересекаетось абсцисс (Рис. 2.15). Таким образом, следующее приближение к стационарной точке определяется по формуле

Если , поиск следует закончить. В противном случае необходимо выбрать одну из точек L или R таким образом, чтобы знаки производной в этой точке и точке z были различны, а затем повторить основной шаг алгоритма. Например, в ситуации, изображенной на Рис. 2.15, в качестве двух следующих точек должны быть выбраны точки z и R. Легко видеть, что в отличие от метода средней точки метод секущих основан на исследовании не только знака, но и значений производной в пробных точках и поэтому в ряде случаев позволяет исключить более половины интервала поиска (см. Рис. 2.15).

Пример 2.7

Минимизировать функцию в интервале , используя Метод секущих

Итерация 1.

Шаг 1. .

Шаг 2

Шаг 3. ; положить R=2.53.

Итерация 2.

Шаг 2

Шаг 3. 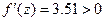; положить R= 1.94.

Итерации продолжаются до тех пор, пока не будет выполняться неравенство .

Поиск по сайту: