Пример 2.1

Рассмотрим функцию

определенную на всей действительной оси. Первая производная этой функции равна

Ясно, что первая производная обращается в нуль в точках х=0, 1,2,3, и, следовательно, эти точки можно классифицировать как стационарные. Вторая производная функции равна

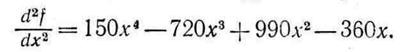
Вычислив значения второй производной в четырех точках х=0, 1,2,3, получим

Отсюда следует вывод, что х=1, 3 — точки локальных минимумов, а х=2 — точка локального максимума. Чтобы идентифицировать точку х=0, вычислим третью производную

Так как эта производная отлична от нуля и имеет нечетный порядок, то точка х=0 является не точкой оптимума, а точкой перегиба.

Следующий вопрос, к рассмотрению которого мы переходим, связан с определением глобального максимума или минимума функции одной переменной. Поскольку глобальный оптимум является локальным, можно вычислить все локальные оптимумы и выбрать из них наилучший. Алгоритм, основанный на этом простейшем подходе, приводится ниже.

Максимизировать f(x) при ограничении ,

где а и b — установленные границы изменения значений переменной х.

Таккак функция исследуется на заданном интервале, нетрудно заметить, что проверку наличия локального оптимума необходимо проводить не только в стационарных точках, но и в граничных точках интервала.

Шаг 1. Приравнять df/dx=0 и найти все стационарные точки.

Шаг 2. Выбрать все стационарные точки, которые расположены в интервале [а, b]. Обозначим эти точки через .

Проверку наличия локального оптимума следует проводить только на множестве указанных точек, дополненном точками а и b.

Шаг 3. Найти наибольшее значение f (х) из множества f(a), f(b), f(х_i),... ,f(х_N),. Это значение соответствует глобальному максимуму.

Примечание. При построении алгоритма мы не пытались классифицировать стационарные точки как точки локального минимума, точки локального максимума или точки перегиба, поскольку для этого требуется вычисление производных высших порядков. Для определения глобального оптимума легче вычислить соответствующие значения функции и выбрать из них максимальное.

Пример 2.2 Максимизировать 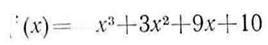на интервале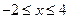

Приравниваем первую производную нулю

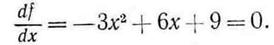
Решая это уравнение, получаем две стационарные точки х=3 и х= -1, которые расположены внутри заданного интервала.

Для того чтобы найти глобальный максимум, вычислим значения f(x) в точках х=3, -1, -2 и 4:

Таким образом, точка х=3 соответствует максимальному значению f на интервале .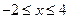

Вместо перебора всех стационарных точек и соответствующих значений функции можно воспользоваться специальными процеду­рами, позволяющими найти глобальный оптимум с меньшими за­тратами времени при условии, что функция обладает определенными ' свойствами. В заключительной части разд. 2.1 было дано определе­ние унимодальной функции, для которой локальный оптимум яв­ляется глобальным. К сожалению, определение унимодальной функ­ции не позволяет непосредственно проверить, является ли функция унимодальной. Однако в теории оптимизации выделяется важный класс унимодальных функций, а именно класс выпуклых и вогнутых функций, которые допускают проверку такого рода. Основные свойства выпуклых и вогнутых функций приведены в приложении Б.

Пример 2.3

Исследуем свойства функции

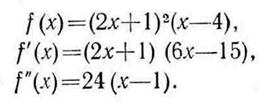
При имеем , и, следовательно, функция является вогнутой в указанной области. Если же , то , т. е. функция является выпуклой в этой области.

Заметим, что функция имеет две стационарные точки х=-0.5 и х=2.5. Поскольку , функция обладает локальным максимумом при х=-0.5. В точке х=2.5 вторая производная , и, следовательно, функция достигает в этой точке локального минимума. Если ограничить допустимую область неравенством , то f(x) имеет глобальный максимум при х=-0.5, так как f(x) — вогнутая функция (в данной области) и х=-0.5 — точка локального максимума. Аналогично если ограничить допустимую область неравенством , то f(x) достигает глобального минимума при х =2.5. Однако если переменная х изменяется на всей действительной оси от — до + , то функция f(x) не имеет конечного глобального максимума или минимума.

Поиск по сайту: