АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Метод Ньютона — Рафсона

Читайте также:
  1. F. Метод, основанный на использовании свойства монотонности показательной функции .
  2. FAST (Методика быстрого анализа решения)
  3. I этап Подготовка к развитию грудобрюшного типа дыхания по традиционной методике
  4. I. 2.1. Графический метод решения задачи ЛП
  5. I. 3.2. Двойственный симплекс-метод.
  6. I. ГИМНАСТИКА, ЕЕ ЗАДАЧИ И МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ
  7. I. Метод рассмотрения остатков от деления.
  8. I. Методические основы
  9. I. Методические основы оценки эффективности инвестиционных проектов
  10. I. Организационно-методический раздел
  11. I. Предмет и метод теоретической экономики
  12. I. Что изучает экономика. Предмет и метод экономики.

В рамках схемы Ньютона - Рафсона предполагается, что функция дважды дифференцируема. Работа алгоритма начинается в точке 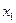, которая представляет начальное приближение (или начальную оценку) координаты стационарной точки, или корня уравнения . Затем строится линейная аппроксимация функции f'(x) в точке 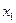, и точка, в которой аппроксимирующая линейная функция обращается в нуль, принимается в качестве следующего приближения.

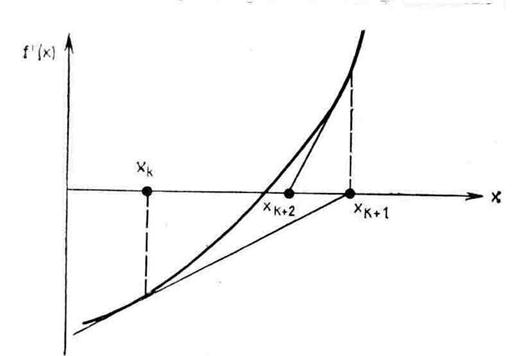
Рис. 2.13. Метод Ньютона — Рафсона (сходимость)

Если точка принята в качестве текущего приближения к стационарной точке, то линейная функция, аппроксимирующая функцию f'(x) в точке записывается в виде

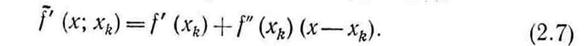
Приравняв правую часть уравнения (2.7) нулю, получим следующее приближение:

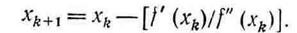
Рис. 2.13 иллюстрирует основные шаги реализации метода Ньютона. К сожалению, в зависимости от выбора начальной точки и вида функции алгоритм может, как сходиться к истинной стационарной точке, так и расходиться, что отражено на Рис. 2.14. Если начальная точка расположена правее , то получаемые в результате последовательных приближений точки удаляются от стационарной точки z.

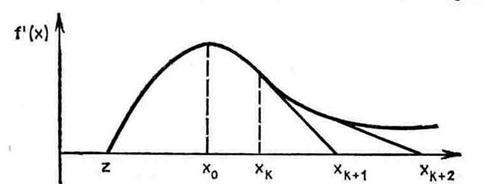
Рис. 2.14. Метод Ньютона — Рафсона (отсутствие сходимости).

Пример 2.6


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)