 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Использование методов оптимизации при проектировании
Сфера применения оптимизационных методов в инженерном проектировании достаточно широка: от проектирования отдельных структурных элементов технических систем до проектирования узлов оборудования и составления предварительных проектов промышленных предприятий в целом. Для того чтобы использовать методы оптимизации, необходимо разработать «принципиальную схему» функционирования системы или выявить ее структуру; тогда задача оптимизации сводится к выбору таких значений переменных, характеризующих размеры отдельных устройств и режимы их работы, которым соответствует наилучшее значение характеристического показателя качества функционирования системы.
Пример 1.1. Проектирование системы снабжения кислородом
Описание задачи. Кислородный конвертер, используемый в производстве стали, представляет собой химический реактор периодического действия, который потребляет чистый кислород. Процесс функционирования конвертера — циклический.

Рис. 1.2. Цикл потребления кислорода, пример 1.1.
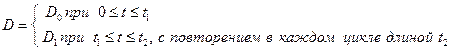
Руда и флюс загружаются в реактор, взаимодействуют в течение определенного периода времени, а затем продукты взаимодействия выводятся наружу. Этот циклический процесс связан с периодическими изменениями скорости потребления кислорода. Как показано на рис. 1.2, каждый цикл состоит из временного интервала длины t1, на котором расход кислорода в единицу времени невелик и равен Do, и временного интервала (t2 - t1), которому соответствует высокая скорость потребления D1. Используемый в конвертере кислород производится на специальной установке в соответствии с распространенным технологическим способом, который позволяет получать кислород из воздуха путем охлаждения и дистилляции. Кислородные установки отличаются высоким уровнем автоматизации и, как правило, имеют постоянную производительность. Для того чтобы соединить непрерывно действующую кислородную установку с циклически функционирующим конвертером, необходимо разработать проект простой системы управления запасами (рис. 1.3), состоящей из компрессора и резервуара для храпения кислорода.

Рис. 1.3. Проект системы снабжения кислородом, пример 1.1.
Рассмотрим возможные проекты. В самом простом случае производительность кислородной установки можно выбрать равной D1, наибольшей скорости потребления кислорода. В течение интервала времени, которому соответствует низкий расход кислорода, излишек газа придется выпускать в атмосферу. С другой стороны, можно выбрать кислородную установку с такой производительностью, которая позволила бы в течение одного цикла получать количество кислорода, требуемое для обеспечения нормальной работы конвертера. В интервале времени, когда расход газа невелик, излишек кислорода под давлением накапливался бы в резервуаре для последующего использования в течение интервала времени, которому соответствует высокая скорость потребления. Все промежуточные проекты отличаются от рассмотренных различными сочетаниями запасов и потерь кислорода. Задача заключается в том, чтобы выбрать оптимальный проект.
Постановка задачи. Изучаемая система состоит из установки для производства кислорода, компрессора и резервуара для хранения газа. Характеристики кислородного конвертера и цикла потребления кислорода предполагаются заданными, так как определяются внешними по отношению к системе факторами. Характеристический показатель качества проекта естественно выбрать в виде полных затрат в единицу времени, которые включают затраты на производство кислорода (постоянные и переменные), затраты на эксплуатацию компрессора, а также постоянные издержки, связанные с приобретением компрессора и резервуара для хранения кислорода. Основными независимыми переменными являются производительность кислородной установки F (кг О2/ч), проектная мощность компрессора Н (л. с.), проектная емкость резервуара V (м3) и максимальное давление в резервуаре р (Н/м2). Предполагается, что кислородная установка является стандартной и поэтому полностью характеризуется своей производительностью. Кроме того, предполагается также, что резервуар отвечает требованиям обычного проекта и предназначен для хранения кислорода.
Модель системы включает основные соотношения, с помощью которых можно описать взаимосвязи между независимыми переменными.
Пусть  - максимальное количество кислорода, запасенного к резервуаре. Используя скорректированное уравнение газового состояния, получим
- максимальное количество кислорода, запасенного к резервуаре. Используя скорректированное уравнение газового состояния, получим

где R — универсальная газовая постоянная, Т — температурагаза(предполагается постоянной), z — коэффициент сжимаемости, М — молекулярный вес кислорода.
Из рис. 1.2 следует, что максимальное количество кислорода, которое должно быть запасено в резервуаре, равняется площади, ограниченной кривой потребления между точками  и
и  , D1 и F. Таким образом,
, D1 и F. Таким образом,

Подставив выражение (1.2) в (1.1), получим

Конструкция компрессора должна обеспечивать управление потоком газа, обладающим скоростью  , и повышение давления газа до максимального значения р. В предположении, что газ идеальный, а процесс сжатия изотермический, имеем [3]
, и повышение давления газа до максимального значения р. В предположении, что газ идеальный, а процесс сжатия изотермический, имеем [3]
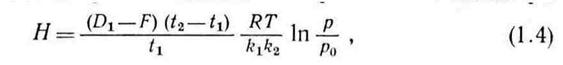
где 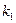 — переводной коэффициент,
— переводной коэффициент,  — коэффициент полезного действия компрессора,
— коэффициент полезного действия компрессора, 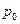 — начальное давление кислорода.
— начальное давление кислорода.
Уравнения (1.3) и (1.4) необходимо дополнить неравенством устанавливающим, что производительность кислородной установки F не должна быть меньше средней скорости потребления кислорода, т. е. неравенством
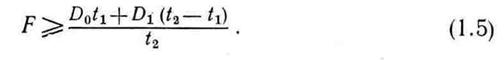
Кроме того, максимальное давление в резервуаре должно превышать начальное давление кислорода:

Характеристический показатель качества проекта включает затраты на производство кислорода:
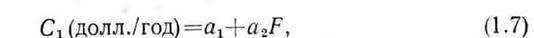
где  и
и 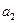 — эмпирически определяемые параметры для установок рассматриваемого типа, связанные с затратами на топливо, воду и рабочую силу.
— эмпирически определяемые параметры для установок рассматриваемого типа, связанные с затратами на топливо, воду и рабочую силу.
Капитальные затраты на приобретение резервуара для хранения кислорода находятся с помощью следующей степенной зависимости:

где 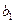 и
и  — эмпирически определяемые постоянные, отражающие специфические особенности конструкции резервуара. Капитальные затраты, связанные с приобретением компрессора, вычисляются с помощью аналогичной формулы:
— эмпирически определяемые постоянные, отражающие специфические особенности конструкции резервуара. Капитальные затраты, связанные с приобретением компрессора, вычисляются с помощью аналогичной формулы:

Затраты на эксплуатацию компрессора приближенно описываются выражением  , где
, где  — затраты на эксплуатацию компрессора единичной мощности в единицу времени. Таким образом, функцию полных издержек можно записать в следующем виде:
— затраты на эксплуатацию компрессора единичной мощности в единицу времени. Таким образом, функцию полных издержек можно записать в следующем виде:
Полные годовые затраты

где N — число циклов потребления кислорода, реализуемых в течение года, d — весовой коэффициент.
Задача оптимизации заключается в том, чтобы минимизировать функцию (1.10) путем соответствующего выбора значений F, V, Н и р, удовлетворяющих уравнениям (1.3) и (1.4), а также неравенствам (1.5) и (1.6).
Решение сформулированной задачи в существенной степени зависит от выбора параметров цикла ( ), стоимостных параметров (
), стоимостных параметров ( ) и физических параметров (
) и физических параметров ( ).
).
В принципе эту задачу можно решить путем исключения V и Н из формулы (1.10) с помощью (1.3) и (1.4); в результате получается задача с двумя переменными. Если затем изобразить линии уровня функции полных затрат на плоскости с координатами F и p, а также учесть неравенства (1.5) и (1.6), то можно найти точку минимума. Однако методы, рассматриваемые ниже, позволяют получить решение с гораздо меньшими затратами труда. Более подробно вопросы, связанные с решением задач с различными значениями параметров, освещены в работе [4].
В примере 1.1 представлена постановка задачи предварительного проектирования системы, состоящей из нескольких агрегатов. Следующий пример иллюстрирует процесс проектирования отдельного структурного элемента системы.
Пример 1.2. Проектирование нагруженной балки
Описание задачи. Балка А крепится на жесткой опоре В с помощью сварного соединения. Балка изготавливается из стали марки 1010 и должна выдерживать нагрузку F=6000 фунт. Размеры балки выбираются таким образом, чтобы полные затраты были минимальными. Схематический чертеж системы приведен на рис. 1.4.

Рис. 1.4. Нагруженная балка, пример 1.2.
Постановки задачи. Определение границ системы в данном случае является тривиальной задачей. Система состоит из балки А и сварного шва, необходимого для прикрепления балки к опоре В. Независимыми, или управляемыми, переменными служат размеры h, l, t и b, которые показаны на
рис. 1.4. Длина балки L предполагается равной 14 дюйм. Для удобства записи представим введенные переменные как компоненты неизвестного вектора х:

Характеристическим показателем качества проекта служат затраты на построение сварной группы. Основными стоимостными характеристиками такой группы являются:
1) затраты на подготовительные работы,
2) затраты на сварочные работы,
3) стоимость материалов.
Следовательно можно записать

где F(x) — функция затрат, с0 — затраты на подготовительные работы; с1— затраты на сварочные работы, с2 — стоимость материалов.
Затраты на подготовительные работы с0. Решение о проектировании рассматриваемого структурного элемента в виде сварного узла было основано на наличии аппарата для сварки прямолинейным швом у заказчика проекта. Далее предположим, что все устройства, необходимые для установки и поддержания балки в положении, удобном для проведения сварочных работ, также имеются в наличии. В этом случае затраты с0 можно не учитывать при построении модели.
Затраты на сварочные работы с1. Предположим, что сварка будет проводиться аппаратом, при использовании которого полные расходы составляют 10 долл./ч (включая эксплуатационные расходы и издержки на техническое обслуживание и текущий ремонт). Далее пусть сварочный аппарат накладывает один кубический дюйм сварного шва за 6 мин. Тогда затраты на сварочные работы равны

где Vw — объем сварного шва в кубических дюймах.
Стоимость материалов с2.
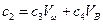 ,
,
где 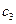 - стоимость/ объем сварного шва = (0.37) (0.283) (долл./дюйм3);
- стоимость/ объем сварного шва = (0.37) (0.283) (долл./дюйм3);  - стоимость / объем балки = (0.17)×(0.283) (долл./ /дюйм3);
- стоимость / объем балки = (0.17)×(0.283) (долл./ /дюйм3); 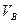 - объем балки А в кубических дюймах. Из геометрических соотношений следует, что
- объем балки А в кубических дюймах. Из геометрических соотношений следует, что

Имеем

Следовательно, функция затрат принимает следующий вид:

или (если выразить ее через переменные х)

Заметим, что все комбинации значений  могут оказаться допустимыми, если балка выдерживает заданную нагрузку. Необходимо построить несколько функциональных соотношений между управляемыми переменными, позволяющих сузить область их допустимых значений. Эти соотношения, записанные в форме неравенств, представляют модель системы. Сначала приведем эти неравенства, а затем интерпретируем их. Имеем
могут оказаться допустимыми, если балка выдерживает заданную нагрузку. Необходимо построить несколько функциональных соотношений между управляемыми переменными, позволяющих сузить область их допустимых значений. Эти соотношения, записанные в форме неравенств, представляют модель системы. Сначала приведем эти неравенства, а затем интерпретируем их. Имеем

где  - расчетное напряжение в сварном шве при сдвиге;
- расчетное напряжение в сварном шве при сдвиге;  — максимальное напряжение в сварном шве при сдвиге, функция от х;
— максимальное напряжение в сварном шве при сдвиге, функция от х;  — расчетное нормальное напряжение для материала балки;
— расчетное нормальное напряжение для материала балки; 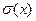 — максимальное нормальное напряжение в балке, функция от х;
— максимальное нормальное напряжение в балке, функция от х;  — критическая нагрузка на балку, функция от х.
— критическая нагрузка на балку, функция от х.  — величина прогиба конца балки, функция от х. Для того чтобы завершить построение модели, необходимо ввести в рассмотрение несколько формул из теории сопротивления материалов.
— величина прогиба конца балки, функция от х. Для того чтобы завершить построение модели, необходимо ввести в рассмотрение несколько формул из теории сопротивления материалов.
Напряжение в сварном шве  . В соответствии с работой [5] напряжение в сварном шве можно разложить на две составляющие
. В соответствии с работой [5] напряжение в сварном шве можно разложить на две составляющие  и
и 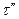 , где
, где  — первичное напряжение в плоскости поперечного сечения сварного шва, а
— первичное напряжение в плоскости поперечного сечения сварного шва, а 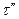 — вторичное напряжение при кручении:
— вторичное напряжение при кручении:

При этом

где М — момент силы F относительно центра тяжести сварной группы, J — полярный момент инерции сварной группы. Напряжение  сварном шве вычисляется в соответствии с формулой
сварном шве вычисляется в соответствии с формулой

где cos q= х2z/2R.
Напряжение при изгибе балки а(х). Можно показать, что максимальное напряжение при изгибе равно

Критическая нагрузка на балку 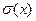 . С ростом отношения
. С ростом отношения 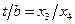 наблюдается тенденция к потере устойчивости балки. Те комбинации значений
наблюдается тенденция к потере устойчивости балки. Те комбинации значений  и
и  , при которых возможна потеря устойчивости, необходимо исключить из числа допустимых. В работе [6] показано,что для балок, близких к прямоугольным, критическая нагрузка приближенно описывается следующим выражением:
, при которых возможна потеря устойчивости, необходимо исключить из числа допустимых. В работе [6] показано,что для балок, близких к прямоугольным, критическая нагрузка приближенно описывается следующим выражением:
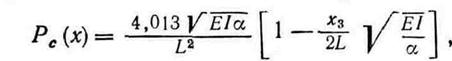
где Е— модуль Юнга == 30×106 фунт/дюйм2,  ,
,  , G— модуль сдвига == 12 106 фунт/дюйм2.
, G— модуль сдвига == 12 106 фунт/дюйм2.
Прогиб балки  . Чтобы вычислить величину прогиба, предположим, что балка представляет собой консоль с вылетом L. Тогда
. Чтобы вычислить величину прогиба, предположим, что балка представляет собой консоль с вылетом L. Тогда
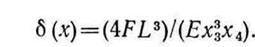
Остальные неравенства интерпретируются следующим образом:
 устанавливает практическую невозможность получения сварного шва, ширина которого превышает ширину балки, a
устанавливает практическую невозможность получения сварного шва, ширина которого превышает ширину балки, a  и
и  отражают требования неотрицательности
отражают требования неотрицательности 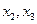 . Заметим, что неотрицательность
. Заметим, что неотрицательность 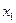 и
и  следует из неравенств
следует из неравенств  и
и  .Ограничение
.Ограничение 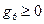 гарантирует, что критическая нагрузка на балку не будет превышена. Неравенство
гарантирует, что критическая нагрузка на балку не будет превышена. Неравенство  отражает тот факт, что физически невозможно сделать сварной шов, ширина которого меньше некоторого порогового значения.
отражает тот факт, что физически невозможно сделать сварной шов, ширина которого меньше некоторого порогового значения.
Наконец, параметры  и
и  , фигурирующие в
, фигурирующие в 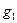 и
и  зависят от материала конструкции. Для стали марки 1010 соответствующие значения этих параметров равны =13 600 фунт/дюйм2 и
зависят от материала конструкции. Для стали марки 1010 соответствующие значения этих параметров равны =13 600 фунт/дюйм2 и  =30 000 фунт/дюйм2.
=30 000 фунт/дюйм2.
Оптимизационная задача проектирования включает функцию затрат (1.12) и сложную систему неравенств, которая получается путем подстановки приведенных выше формул в (1.13)—(1.20). При этом все функции оказываются выраженными через четыре независимые переменные.
Данная задача достаточно сложна и, как легко видеть, не может быть решена графическим способом. Однако оптимальный проект нетрудно получить с помощью численных методов, рассматриваемых в последующих главах.
Более подробное обсуждение этой задачи и методов ее решения можно найти в [7].
1.2.2 Использование методов оптимизации при планировании и анализе функционирования систем
Вторая важная область применения оптимизационных методов в инженерной практике связана с совершенствованием существующих систем и разработкой производственных планов для многопродуктовых технико-экономических процессов. Задачи анализа функционирования систем обычно возникают в тех случаях, когда требуется адаптировать существующую производственную систему к новым условиям функционирования, отличным от тех условий, которые были предусмотрены проектом этой системы. Причины, порождающие требования такого рода, как правило, связаны с необходимостью
1) увеличения общего объема выпуска продукции;
2) использования других видов сырья и расширения ассортимента изделий;
3) совершенствования технологических операций, отличающихся низким уровнем проектных решений.
В связи с решением указанных задач требуется выбрать новый температурный режим, давление или характеристики потока; установить дополнительное оборудование; разработать новые технологические операции. Методы оптимизации в производственном планировании ориентированы главным образом на составление программ производства нескольких видов продукции на отдельном предприятии, а также на координирование производственных планов предприятий, которые связаны хозяйственными отношениями. Поскольку в таких приложениях предполагается, что основное оборудование установлено и функционирует, предметом исследования являются только функции переменных затрат.

Рис. 1.5. Схема к задаче планирования нефтеперерабатывающего производства, пример 1.3.
Возникающие при этом задачи чаще всего можно сформулировать с помощью линейных и квазилинейных моделей. В качестве иллюстрации этого класса приложений оптимизационных методов рассмотрим задачу планирования производства нефтепродуктов.
Пример 1.3. Планирование производства нефтепродуктов
Описание задачи. В процессе переработки сырой нефти производится определенное количество бензиновых полупродуктов, которые затем последовательно смешиваются с целью получения двух видов топлива для двигателей внутреннего сгорания — обычного топлива и топлива высшего качества. Для каждого полупродукта известны значение показателя его эффективности, максимальный выход и фиксированная цена единицы объема полупродукта. Для каждого вида топлива установлены минимальное значение показателя эффективности и продажная цена, а также известны удельные затраты на смешивание топлива. Минимальный уровень производства обоих видов топлива определяется договорными обязательствами. Остальное произведенное топливо и неиспользованные полупродукты могут быть реализованы посредством свободной продажи по известным ценам. Требуется составить оптимальный план производства топлива в течение заданного периода времени.
Постановка задачи. На схеме, изображенной на рис.1.5, показано что исследуемая система включает ряд бензиновых полупродуктов, технологическую операцию смешивания и два вида жидкого моторного топлива. Процессы переработки нефти и производства полупродуктов исключены из рассмотрения наряду с подсистемами управления запасами и распределения сырой нефти, полупродуктов и конечной продукции. Поскольку оборудование, необходимое для выполнения операции смешивания, к началу планового периода установлено и функционирует, следует рассмотреть только стоимостные характеристики производственного процесса.
Характеристическим показателем качества функционирования системы в данном случае является чистая прибыль, реализуемая в течение планового периода. Чистая прибыль состоит из дохода от продажи топлива и полупродуктов за вычетом затрат на смешивание и производство полупродуктов. Независимые переменные выражают величины потоков по ориентированным дугам, изображенным на рис. 1.5. Таким образом, с каждым из полупродуктов ассоциированы три переменные. Одна из переменных выражает количество полупродукта, направляемого на производство обычного топлива, вторая — количество полупродукта, направляемого на производство топлива высшего качества, и третья — количество полупродукта, поступающею в свободную продажу.
Итак, для каждого полупродукта с номером i
х i,— количество полупродукта, используемого для производства обычного топлива,
yi— количество полупродукта, используемого для производства топлива высшего качества,
zi— количество полупродукта, направляемого в свободную продажу.
С каждым видом производимого топлива в свою очередь ассоциированы две переменные, одна из которых представляет количество топлива, продаваемого по договорам, а другая — количество топлива, поступающего в свободную продажу.
Таким образом, для каждого вида топлива с номером j
иj — количество топлива, продаваемого по договорам,
vj — количество топлива, поступающего в свободную продажу.
В модель следует включить балансовые соотношения для каждого полупродукта и каждого вида топлива, ограничения, связанные с технологической операцией смешивания и позволяющие учесть заданные уровни эффективности двух видов топлива, а также ограничения, вытекающие из наличия договорных обязательств.
1. Балансовое соотношение для полупродукта с номером i записывается в виде неравенства

где  — выход полупродукта i за плановый период.
— выход полупродукта i за плановый период.
2. Балансовые соотношения для конечной продукции имеют следующий вид:
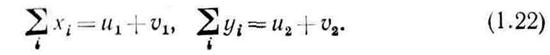
3. Технологические ограничения, связанные с операцией смешивания, записываются в виде
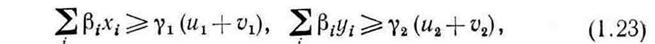
где 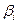 ,— значение показателя эффективности полу продукта i, а
,— значение показателя эффективности полу продукта i, а 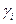 — минимальное значение показателя эффективности топлива вида j.
— минимальное значение показателя эффективности топлива вида j.
4. Ограничение, обусловленное договорными обязательствами, для топлива вида j задается неравенством

где  - минимальный объем производства топлива вида, предусмотренный договорами.
- минимальный объем производства топлива вида, предусмотренный договорами.
Характеристический показатель качества функционирование системы (чистая прибыль) определяется выражением

где 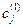 продажная цена единицы конечной продукции вида j в соответствии с договорами;
продажная цена единицы конечной продукции вида j в соответствии с договорами;  — рыночная цена единицы конечной продукции вида j;
— рыночная цена единицы конечной продукции вида j;  — рыночная цена единицы полупродукта i,
— рыночная цена единицы полупродукта i,  — затраты на производство единицы полупродукта i.
— затраты на производство единицы полупродукта i. 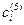 — технологические затраты на смешивание в расчете на единицу полупродукта i.
— технологические затраты на смешивание в расчете на единицу полупродукта i.
С учетом данных, приведенных в табл. 1.1, задача планирования принимает следующий вид:

при следующих ограничениях:
ограничения типа (1.21):

ограничения типа (1.22):
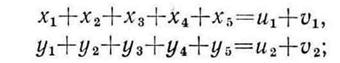
ограничения типа (1.23):

ограничения типа (1.24):
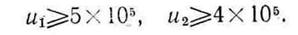


Кроме того, все переменные должны принимать неотрицательные значения; в противном случае решение задачи может и не иметь «физической» интерпретации. В целом задача оптимизации включает 19 переменных и 11 ограничений, а также условия неотрицательности переменных. Заметим, что все фигурирующие в модели функции являются линейными относительно независимых переменных.
Вообще говоря, в процессе нефтепереработки производится значительно большее количество различных полупродуктов и видов конечной продукции, чем это предполагалось в рассмотренном примере. Кроме того, в ряде практических ситуаций целесообразно ввести дополнительные переменные, отражающие динамику управления запасами, а также расширить модельные построения на несколько последовательных плановых периодов. В последнем случае каждая переменная должна быть снабжена вторым индексом, например:
 — количество полупродукта i, используемое для производства обычного топлива в плановом периоде k.
— количество полупродукта i, используемое для производства обычного топлива в плановом периоде k.
При этом размерность результирующей модели производственного планирования существенно возрастает. На практике решение задач такого типа с числом переменных, превышающим тысячу, осуществляется на основе специальных алгоритмов.
Поиск по сайту: