Методы оценивания с использованием квадратичной аппроксимации

Простейшим вариантом полиномиальной интерполяции является квадратичная аппроксимация, которая основана на том факте, что функция, принимающая минимальное значение во внутренней точке интервала, должна быть, по крайней мере, квадратичной. Если же функция линейная, то ее оптимальное значение может достигаться только в одной из двух граничных точек интервала. Таким образом, при реализации метода оценивания с использованием квадратичной аппроксимации предполагается, что в ограниченном интервале можно аппроксимировать функцию квадратичным полиномом, а затем использовать построенную аппроксимационную схему для оценивания координаты точки истинного минимума функции.

Если задана последовательность точек и известны соответствующие этим точкам значения функции ,- то можно определить постоянные величины таким образом, что значения квадратичной функции

совпадут со значениями f(х) в трех указанных точках. Перейдем к вычислению q (x) в каждойиз трех заданных точек. Прежде всего, так как

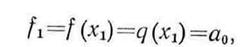
имеем . Далее, поскольку

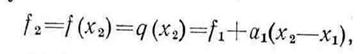
получаем .

Наконец, при

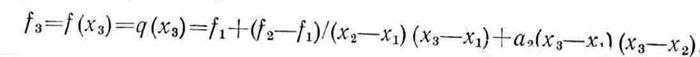
Разрешая последнее уравнение относительно 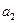получаем

Таким образом, по трем заданным точкам и соответствующим значениям функции можно оценить параметры и из аппроксимирующего квадратичного полинома с помощью приведенных выше формул.

Если точность аппроксимации исследуемой функции в интервале от 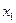до с помощью квадратичного полинома оказывается достаточно высокой, то в соответствии с предложенной стратегией поиска построенный полином можно использовать для оценивания координаты точки оптимума. Напомним, что стационарные точки функции одной переменной определяются путем приравнивания к нулю ее первой производной и последующего нахождения корней полученного таким образом уравнения. В данном случае из уравнения

можно получить

Поскольку функция f(x) на рассматриваемом интервале обладает свойством унимодальности, а аппроксимирующий квадратичный полином также является унимодальной функцией, то можно ожидать, что величина окажется приемлемой оценкой координаты точ­ки истинного оптимума л;*.

Пример 2.4

Рассчитать координату точки минимума функции при использовании квадратичной аппроксимации в интервале .

Пусть , , а 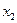есть средняя точка интервала, т. е. . Вычислим соответствующие значения функции:

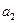Для того чтобы оценить , необходимо найти значения параметров и аппроксимирующей функции. Имеем

Подстановка этих значений в формулу для позволяет получить

Точный минимум достигается при =1.5874.

Поиск по сайту: