Критерии оптимальности. При анализе оптимизационных задач, как правило, возникают два общих вопроса

При анализе оптимизационных задач, как правило, возникают два общих вопроса.

1. Вопрос анализа «в статике». Как определить, представляет ли данная точка х* оптимальное решение задачи?

2. Вопрос анализа «в динамике». Если х* не является точкой оптимума, то какая последовательность действий приводит к полу­чению оптимального решения?

В этом разделе основное внимание уделяется решению вопроса диализа «в статике», а именно построению множества критериев оптимальности, позволяющих определить, является ли данное ре­шение оптимальным.

Определения.

Функция f(x), определенная на множестве S, достигает своего глобального минимума в точке 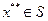в том и только том случае, если

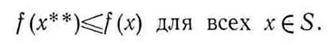
Функция f(x), определенная на множествеS, имеет локальный минимум (относительный минимум) в точке 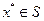в том и только том случае, если

для всех х, удаленныхот х* на расстояние, меньшее 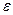, т. е. если существует 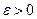, такое, что для всех х, удовлетворяющих условию 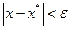, выполняется неравенство .

Поиск по сайту: