Пример 2.4. Задача управления запасами

Многие фирмы создают запасы производимых товаров для удовлетворения, будущего спроса. Среди причин, обусловливающих содержание запасов в определенном объеме, можно отметить нерациональные потери времени и средств, связанные с их непрерывным пополнением. С другой стороны, пополнение запасов через продолжительные промежутки времени приводит к образованию чрезмерно больших запасов, которое требует необоснованных капитальных затрат и значительно повышает стоимость хранения запасов. Определение оптимального объема запасов представляет собой классическую задачу оптимизации, для решения которой часто используется так называемая модель определения наиболее экономичного размера заказа.

В рамках этой модели спрос предполагается постоянным и равным единиц товара в год. Частое пополнение запасов нецелесообразно, так как стоимость выполнения одного заказа составляет К долл. независимо от его размера. Первоначальная стоимость единицы товара равна с долл. Хранение излишних запасов также нецелесообразно, поскольку стоимость хранения единицы товара отлична от нуля и составляет h долл. в год. Для того чтобы упростить задачу, предположим, что спрос удовлетворяется немедленно (т. е. одолженные заказы отсутствуют), а пополнение осуществляется сразу же, как только запасы иссякают.

Рис. 2.9 иллюстрирует изменение объема запасов с течением времени. В точке А объем запасов равен В, затем объем запасов начинает уменьшаться со скоростью единиц товара в единицу времени и достигает нулевого значения в точке С. В это время поступает новая партия товара, и объем запасов восстанавливается.

Треугольник АВС представляет один цикл управления запасами, который повторяется во времени. Задача заключается в том, чтобы определить оптимальный размер заказа В и продолжительность интервала времени между заказами С—А. Обозначим соответствующие переменные через Q и Т.

Поскольку Т есть величина промежутка времени, в течение которого при скорости расходования К истощается запас Q, имеем T==Q/l. Таким образом, задача сводится к нахождению оптимального значения Q. Заметим, что когда Q мало, переменная Т также принимает малое значение. При этом частота заказов велика, что обусловливает большие затраты на выполнение заказов и относительно малые издержки хранения запасов.

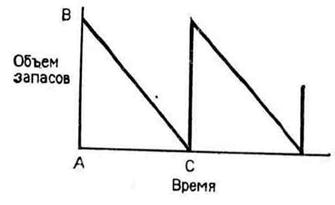
Рис. 2.9. Циклы управления запасами

С другой стороны, наличие большого объема запасов (Q велико) приводит к увеличению затрат на хранение запасов и одновременно к снижению издержек, связанных с выполнением заказов на товары. Одна из основных задач управления запасами состоит в определении оптимального значения Q, которому соответствует минимум суммы полных годовых затрат.

Получим аналитическое выражение для функции полных годовых затрат (затраты/цикл х количество циклов/год).

Количество циклов (заказов)/год=1/Т==l/Q,

Затраты/цикл = Затраты па выполнение заказов +

+ Затраты на хранение запасов =

=(K+cQ)+ [ (Q/2)hT ] =

=K+cQ+ (hQ²/2 l).

Примечание. Затраты на хранение запасов в течение цикла равны затратам на хранение Q/2 единиц товара в течение интервала времени Т.

Таким образом, подлежащая минимизации функция полных затрат есть

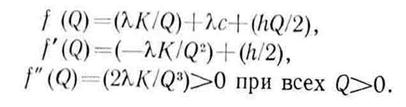
Отсюда следует, что f(Q) — выпуклая функция и если существует положительное значение Q*, такое, что f' (Q*)=0, то Q* минимизирует f(Q).

Решив уравнение f' (Q)=0, получим

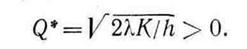
Таким образом, оптимальный размер заказа равен

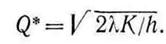
При этом Т*=(2K/hl)^0.5 - интервал времени между заказами. Величина Q* известна в теории управления запасами как наиболее экономичный размер заказа.

Поиск по сайту: