 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Поиск с помощью метода золотого сечения
Из проведенного выше обсуждения методов исключения интервалов и минимаксных стратегий поиска можно сделать следующие выводы.
1. Если количество пробных точек принимается равным двум, то их следует размещать на одинаковых расстояниях от середины интервала.
2. В соответствии с общей минимаксной стратегией пробные точки должны размещаться в интервале по симметричной схеме, таким образом, чтобы отношение длины исключаемого подынтервала к величине интервала поиска оставалось постоянным.

Рис. 2.10. Поиск с помощью метода золотого сечения.
3. На каждой итерации процедуры поиска должно вычисляться только одно значение функции в получаемой точке.
Руководствуясь этими выводами, рассмотрим симметричное расположение двух пробных точек па исходном интервале единичной длины, которое показано на Рис. 2.10. (Выбор единичного интервала обусловлен соображениями удобства.) Пробные точки отстоят от граничных точек интервала на расстоянии  . При таком симметричном расположении точек длина остающегося после исключения интервала всегда равна
. При таком симметричном расположении точек длина остающегося после исключения интервала всегда равна  независимо от того, какое из значений функции в пробных точках оказывается меньшим. Предположим, что исключается правый подынтервал. На Рис. 2.11 показано, что оставшийся подынтервал длины
независимо от того, какое из значений функции в пробных точках оказывается меньшим. Предположим, что исключается правый подынтервал. На Рис. 2.11 показано, что оставшийся подынтервал длины  содержит одну пробную точку, расположенную па расстоянии(1-
содержит одну пробную точку, расположенную па расстоянии(1-  ) от левой граничной точки.
) от левой граничной точки.
Для того чтобы симметрия поискового образца сохранялась, расстояние (1—т) должно составлять  -ю часть длины интервала (которая равна
-ю часть длины интервала (которая равна  ). При таком выборе
). При таком выборе  следующая пробная точка размещается на расстоянии, равном
следующая пробная точка размещается на расстоянии, равном  -й части длины интервала, от правой граничной точки интервала (Рис. 2.12).
-й части длины интервала, от правой граничной точки интервала (Рис. 2.12).

Рис. 2.11. Интервалы, полученные методом золотого сечения.
Отсюда следует, что при выборе  в соответствии с условием
в соответствии с условием  симметрия поискового образца, показанного на Рис. 2.10, сохраняется при переходе к уменьшенному интервалу, который изображен на Рис. 2.12. Решая это квадратное уравнение, получаем
симметрия поискового образца, показанного на Рис. 2.10, сохраняется при переходе к уменьшенному интервалу, который изображен на Рис. 2.12. Решая это квадратное уравнение, получаем

откуда положительное решение  =0.61803.... Схема поиска, при которой пробные точки делят интервал в этом отношении, известна под названием поиска с помощью метода золотого сечения.
=0.61803.... Схема поиска, при которой пробные точки делят интервал в этом отношении, известна под названием поиска с помощью метода золотого сечения.

Рис. 2.12. Симметрия золотого сечения интервала
Заметим, что после первых двух вычислений значений функции каждое последующее вычисление позволяет исключить подынтервал, величина которого составляет (1—  )-ю долю от длины интервала поиска. Следовательно, если исходный интервал имеет единичную длину, то величина интервала, полученного в результате N вычислений значений функции, равна
)-ю долю от длины интервала поиска. Следовательно, если исходный интервал имеет единичную длину, то величина интервала, полученного в результате N вычислений значений функции, равна  . Можно показать, что поиск с помощью метода золотого сечения является асимптотически наиболее эффективным способом реализации минимаксной стратегии поиска.
. Можно показать, что поиск с помощью метода золотого сечения является асимптотически наиболее эффективным способом реализации минимаксной стратегии поиска.
Пример 2.3
Минимизировать функцию  в интервале (60;150), используя Метод золотого сечения
в интервале (60;150), используя Метод золотого сечения
Для того чтобы перейти к интервалу единичной длины, проведем замену переменной, положив  . Таким образом, задача принимает следующий вид:
. Таким образом, задача принимает следующий вид:
Минимизировать 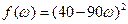
при ограничении  .
.
Итерация 1.
 . Проведем два первых вычисления значений функции:
. Проведем два первых вычисления значений функции:

Так как 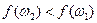 и
и  интервал
интервал  исключается.
исключается.
Итерация 2.
 . Следующее вычисление значения функции проводится в точке
. Следующее вычисление значения функции проводится в точке
 .
.
Так как 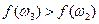 и
и 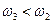 интервал
интервал  исключается.
исключается.
Итерация 3.
 . Следующее вычисление значения функции проводится в точке, расположенной на расстоянии
. Следующее вычисление значения функции проводится в точке, расположенной на расстоянии  х (длина полученного интервала) от левой граничной точки интервала, или на расстоянии (1—
х (длина полученного интервала) от левой граничной точки интервала, или на расстоянии (1—  ) х (длина интервала)от правой граничной точки. Таким образом,
) х (длина интервала)от правой граничной точки. Таким образом,
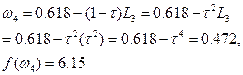
Так как  и
и  , интервал
, интервал 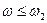 исключается. В результате получен следующий интервал неопределенности:
исключается. В результате получен следующий интервал неопределенности:
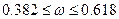 для переменной
для переменной  , или
, или  для переменной х.
для переменной х.
Если в процессе поиска проведено шесть вычислений значений функции, то длина результирующего интервала для переменной  равна
равна
 ,
,
что соответствует интервалу длины 8.1 для переменной х. Для сравнения напомним, что в аналогичной ситуации метод деления интервала пополам привел к получению интервала длины 11.25.
В общем случае если правая и левая граничные точки интервала неопределенности (обозначим их через XR и XL) известны, то координаты всех последующих пробных точек, получаемых в соответствии с методом золотого сечения, можно вычислить по формулам
 или
или 
в зависимости от того, какой подынтервал был исключен на предыдущей итерации — левый или правый. В приведенных выше формулах через  обозначена п-я степень
обозначена п-я степень  , где п — количество вычислений значений функции.
, где п — количество вычислений значений функции.
Поиск с помощью метода золотого сечения может быть окончен либо исходя из заданного количества вычислений значений функции (и, следовательно, величины интервала неопределенности), либо по достижении относительной точности искомого значения функции. Наиболее предпочтительным является использование обоих критериев одновременно.
Название "золотое сечение" произошло от названия соотношения в уравнении
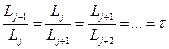
Видно, что  делится на две части так, что отношение целого к большей части равно отношению большей части к меньшей, т.е. равно так называемому золотому отношению"".
делится на две части так, что отношение целого к большей части равно отношению большей части к меньшей, т.е. равно так называемому золотому отношению"".
Поиск по сайту: