 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Анализ инвестиционной и инновационной деятельности
9.1. Классификация инвестиций и основы принятия решений по ним
Все предприятия в той или иной степени связаны с инвестиционной деятельностью. Принятие решений по инвестированию осложняется различными факторами: видом инвестиций; стоимостью инвестиционного проекта; множественностью доступных проектов; ограниченностью финансовых ресурсов, доступных для инвестирования; риском, связанным с принятием того или иного решения, и т. п.
Причины, обусловливающие необходимость инвестиций, могут быть различны, однако в целом их можно подразделить на три вида:
♦ обновление имеющейся материально-технической базы;
♦ наращивание производственной деятельности;
♦ освоение новых видов деятельности.
Степень ответственности за принятие инвестиционного проекта в рамках того или иного направления различна. Так, если речь идет о замещении имеющихся производственных мощностей, решение может быть принято достаточно безболезненно, поскольку руководство ясно представляет себе, в каком объеме и с какими характеристиками необходимы новые основные средства.
Задача осложняется, если речь идет об инвестициях, связанных с расширением основной деятельности, поскольку в этом случае необходимо учесть целый ряд новых факторов: возможность изменения положения фирмы на рынке товаров; доступность дополнительных объемов материальных, трудовых и финансовых ресурсов; возможность освоения новых рынков и др.

 Раздел 9. Анализ инвестиционной и инновационной деятельности
Раздел 9. Анализ инвестиционной и инновационной деятельности
В условиях рыночной экономики возможностей для инвестирования достаточно много. Вместе с тем любое предприятие имеет ограниченные свободные финансовые ресурсы, доступные для инвестирования. Поэтому возникает задача оптимизации инвестиционного портфеля.
Под инвестициями понимается совокупность затрат, реализуемых в форме долгосрочных вложений собственного или заемного капитала.
В основе процесса принятия управленческих решений инвестиционного характера лежат оценка и сравнение объемов предполагаемых инвестиций и будущих денежных поступлений. Поскольку сравниваемые показатели относятся к различным моментам времени, ключевой проблемой здесь является проблема их сопоставимости.
В зависимости от направления вложений капитала различают следующие виды инвестиций:
а) материальные инвестиции - вложения в вещественные эле
менты (в земельные участки, здания, сооружения, в оборудование,
антиквариат, картины и т. д.);
б) финансовые инвестиции - вложения в ценные бумаги (акции,
облигации, закладные бумаги), банковские депозиты и др.;
в) нематериальные инвестиции - вложения в развитие духовных
производительных сил и интеллектуального потенциала (в научные
исследования и разработки, индустрию знаний и повышение ква
лификации, в лицензии и др.).
В производственной сфере материальные инвестиции различаются также в зависимости от того, куда направляются данные вложения: на возмещение потребленного основного капитала (инвестиции на обновление) или на расширение парка оборудования (инвестиции на расширение). Оба вида инвестиций относятся к валовым инвестициям (брутто-инвестиции). Если инвестиции на обновление способствуют увеличению производительности труда, считают, что это инвестиции на рационализацию производства; при этом неизменный результат по выпуску продукции достигается с меньшим объемом рабочей силы.
Финансовый анализ
Важнейшая задача анализа и планирования инвестиций заключается в том, чтобы ответить на вопросы:
♦ является ли данная инвестиция выгодной;
♦ какая из рассматриваемых возможных инвестиций является наиболее оптимальной.
Исходным пунктом большинства методов анализа и планирования инвестиций является предположение о том, что денежные вложения, которые выплачиваются «сегодня», имеют другую реальную ценность, чем равные вложения, выплачиваемые «завтра». Фактор времени отражается в разной стоимости денежных средств, относящихся к различным моментам времени. Это объясняется тем, что имеющиеся в настоящий момент денежные средства могут быть инвестированы и принести доход в будущем. Поэтому денежные средства, не инвестированные сегодня, не принесут доход в будущем и со временем обесценятся.
В общем виде это выражается в следующем:
1) имеющаяся сегодня начальная сумма (Kq) по прошествии п
лет приобретает новую стоимость (наращение):
 (9.1)
(9.1)
где i - процентная ставка за год.
То есть для решения этой задачи применяется математическая модель, называемая «накопленной суммой единицы», или множителем наращения. Для определения прироста суммы применяется формула расчета сложного процента (1 + i)";
2) чтобы получить через п лет новую будущую стоимость (Кп), мы
должны сегодня располагать начальной суммой (К0), которая
насчитывается по (boDMVjre (скипка):

Мы называем вычисление текущей дисконтированной стоимости дисконтированием (discounting), в то время как обратный процесс (вычисление будущей стоимости) называется компаундингом (compounding). Простые математические формулы позволяют нам
Раздел 9. Анализ инвестиционной и инновационной деятельности
извлечь рыночную стоимость любой суммы, которая будет получена или выплачена в любой момент, будь-то настоящее время или определенная дата в будущем.
Дисконтные факторы публикуются также в так называемых таблицах текущей стоимости, по которым аналитики вычисляют текущую стоимость.
К примеру, должник предлагает своему кредитору произвести платеж в сумме 100 усл. ед. не через год, а сегодня, но при этом просит предоставить с этой суммы скидку в размере 4 усл. ед. Кредитор соглашается на это предложение, проведя следующие вычисления. Предположим, он открывает в своем банке сберегательный счет на год, внеся 96 усл. ед. под 6 % годовых (/ = 0,06). Если банк начисляет проценты на сумму вклада каждый год, то на счете через год будет сумма:

С точки зрения кредитора, следовательно, 96 усл. ед. сегодня означают большую стоимость, чем 100 усл. ед., но уже через год.
Кредитор мог бы свои размышления построить и другим образом: будущую стоимость в 100 усл. ед. он мог бы получить при банковской ставке в 6% годовых, если бы на сберегательный счет внес сегодня сумму в размере:

Так как должник дает 96 усл. ед., т. е. большую сумму, то кредитор вполне может согласиться с предложением должника.
Проблема «деньги - время» не нова, поэтому разработаны удобные модели и алгоритмы, позволяющие ориентироваться в истинной цене будущих дивидендов с позиции текущего момента как с привлечением таблиц текущей стоимости, так и компьютерных средств.
Финансовый анализ
9.2. Операции наращивания и дисконтирования в инвестиционном анализе
Логика построения основных алгоритмов достаточно понятна и основана на следующей идее. Простейшим видом финансовой сделки является однократное предоставление в долг некоторой суммы (PV) с условием, что через некоторое время t будет возвращена сумма FV. Эффективность подобной сделки может быть охарактеризована одной из двух величин: темп прироста:

В финансовых расчетах первый показатель (г() имеет еще название «процент», «рост», «ставка процента», «норма доходности», а второй - «дисконт», «ставка дисконтирования», «коэффициент дисконтирования». Очевидно, что обе ставки взаимосвязаны:

Оба показателя могут выражаться либо в долях единицы, либо в процентах. Различие в этих формулах состоит в том, какая величина берется за базу сравнения: в формуле (9.2) - исходная сумма, в формуле (9.3) - возвращаемая сумма.
Итак, в любой простейшей финансовой сделке всегда присутствуют три величины, две из которых заданы, а одна является искомой.
Процесс, в котором заданы исходная сумма и процентная ставка, в финансовых вычислениях называется процессом наращивания, или компаундинга. Процесс, в котором задана возвращаемая сумма и коэффициент дисконтирования, называется процессом дисконти-
Раздел 9. Анализ инвестиционной и инновационной деятельности
рования. В первом случае речь идет о движении денежного потока от настоящего к будущему, во втором - о движении от будущего к настоящему {рис. 9.1).

Рис. 9.1. Логика финансовых операций
Экономический смысл финансовой операции, задаваемой формулой (9.2), состоит в определении величины той суммы, которой будет или желает располагать инвестор по окончании этой операции.
Поскольку из формулы (9.2)
FV = PV + PV-r{t),
и PV ■ nt\ > 0 > то можно наглядно представить, что время генерирует деньги.
На практике норма доходности является величиной непостоянной, зависящей главным образом от степени риска, ассоциируемого с данным видом бизнеса, в который инвестирован капитал (чем выше степень риска, тем выше норма доходности). К примеру, наименее рискованными являются вложения в государственные ценные бумаги или в Нацбанк, однако норма доходности в этом случае относительно невысока.
Финансовый анализ
Коэффициент дисконтирования показывает, какой ежегодный процент возврата хочет (или может) иметь инвестор на инвестируемый им капитал. При этом искомая величина (PV) показывает как бы текущую, «сегодняшнюю» стоимость будущей величины {FV).
Дисконт, связанный с суммовыми величинами (9.3), используется главным образом в операциях по учету векселей банком, т. е. в том случае, если владелец векселя на сумму FV предъявляет его банку, который соглашается учесть его, т. е. купить, удерживая в свою пользу часть вексельной суммы, нередко также называемой дисконтом. В этом случае банк предлагает владельцу сумму (Р V), исчисляемую исходя из объявленной банком ставки дисконтирования (d,tX Расчет этой суммы ведется по формуле, вытекающей из (9.3):

К примеру, векселедержатель предъявил для учета вексель на сумму 10 тыс. грн со сроком погашения 15.04.2000 г. Вексель предъявлен 31.03.2000 г. Банк согласился учесть вексель с дисконтом в 65% годовых. Тогда дисконтная ставка на 15 дней составит (15/360) • 0,65= = 0,027083. Следовательно, сумма, которую векселедержатель может получить от банка, рассчитывается по формуле (9.4):

Комиссионные, удерживаемые банком в свою пользу за предоставленную услугу, в данном примере составили разницу между FV и PV, или 270 грн 83 кои.

Стандартным временным интервалом в финансовых операциях является 1 год. Существует две основные схемы наращения капитала:
♦ схема простых процентов;
♦ схема сложных процентов.
Раздел 9. Анализ инвестиционной и инновационной деятельности
Если исходный инвестируемый капитал равен Р, а требуемая норма доходности за 1 год - г (как коэффициент в долях единицы от начальной суммы Р), тогда считается, что инвестиция сделана на условиях простого процента, если инвестированный капитал ежегодно увеличивается на величину (Р • г). Таким образом, размер
MHRprTMTTT/гпннпгп капитала Р чрпр.ч п тгрт (wttpt палрн-

Если очередной годовой доход исчисляется не с исходной величины инвестированного капитала, а с общей суммы, включающей также и ранее начисленные и не востребованные инвестором проценты, то в этом случае инвестиция сделана на условиях сложного процента. В этом случае размер инвестированного капитала будет равен к концу первого, второго и и-ного года соответственно:

Инвестирование на условиях сложного процента более выгодно, т. к. (1 + г)" > 1 + г • п, то есть Рп на условиях простого процента меньше Рп на условиях сложного процента при п > 1.
В первом случае, при применении простого процента, доходы по мере их начисления целесообразно снимать для потребления или новой инвестиции, а во втором случае - при использовании сложного процента - инвестированный капитал непрерывно генерирует доходы и постоянно возрастает, поэтому объективной необходимости изъятия начисленных процентов для использования в других инвестиционных проектах не возникает.
Формула (9.6) является базовой в финансовых вычислениях. Для удобства пользования ею значения факторного множителя
Финансовый анализ
(FM), обеспечивающего наращивание стоимости, табулированы для различных значений г и п. При пользовании такими таблицами формула (9.6) имеет вид:

где FMhr и) = (1 + г)" - факторный множитель, экономический смысл которого состоит в следующем: он показывает, чему будет равна одна денежная единица (1 гривня, 1 доллар и т. п.) через п периодов при заданной процентной ставке г на каждый из этих периодов.
Схема простых процентов используется в практике банковских расчетов при начислении процентов по краткосрочным ссудам (со сроком погашения до 1 года).
К примеру, выдана ссуда в размере 10 тыс. грн на один месяц (30 дней) под 130% годовых. Тогда размер платежа к погашению составит:


|
В практике вложений нередко используются внутригодовые процентные начисления, т. е. при выплате дивидендов на вложенный капитал нередко оговаривается не только величина годового процента, но и частота выплаты в течение года. В этом случае расчет ведется по формуле сложных процентов по подинтервалам и по ставке, равной пропорциональной доле исходной годовой ставки:
К примеру, в банковский депозит вложены деньги в сумме 10 тыс. грн на 2 года с полугодовыми начислениями процентов под 20% годовых. В этом случае начисление процентов производится 4 раза (2 раза в год в течение 2 лет) по ставке 10% на полугодие (20%: 2). Если воспользоваться формулой (9.7), то сумма к концу двухлетнего периода составила бы:
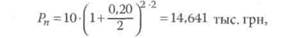
О on где -4— - норма доходности в долях единицы в расчете на одно
полугодие.
Можно сделать вывод, что чем чаще начисляются проценты, тем большая будет итоговая сумма при использовании формулы сложных процентов (т. е. в этом случае 12% годовых не эквивалентны 1% в месяц, а несколько больше при помесячном их начислении по формуле сложных процентов).
Наращивание суммы к исходной инвестиции (вложению) происходит различными темпами в зависимости от частоты начисления процентов, причем с возрастанием частоты накопления сумма увеличивается.
Максимально возможное наращивание реализуется при бесконечном лпоблении голового интегжала Так как

(это важнейшая постоянная математического анализа, относящаяся к группе замечательных пределов - трансцендентное число г = 2,718281, одновременно является основанием натурального логарифма).
пр______

В пределах одного года при непрерывном начислении процентов можно использовать формулу (п = 1):

Финансовый анализ
Возможности использования в контрактах на инвестиции (вложения) различных схем начисления процентов определяют объективную потребность и необходимость сравнительного анализа эффективности таких вложений с использованием некого универсального показателя для любой из схем начисления.
В сравнительном анализе эффективности вложений используют показатель эффективной годовой процентной ставки г,еу обеспечивающий переход от Р к Рп при заданных значениях этих показателей.
В рамках одного года, исходя из формулы (9.7), такой переход
пряттитдатгя чяямгммогтып-

Сравнив эти формулы, получим:
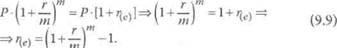
Можно сделать вывод, что эффективная годовая ставка зависит от количества внутригодовых начислений, с ростом которых она также увеличивается.
К примеру, у частного предпринимателя есть возможность получить ссуду на разных условиях:
1) на условиях ежеквартального начисления процентов из расчета 80% годовых;
2) на условиях полугодового начисления процентов из расчета 85% годовых.
Чтобы выяснить, какой вариант более предпочтителен, необходимо рассчитать относительные расходы предпринимателя по обслуживанию ссуды, величина которых оценивается эффективной годовой процентной ставкой. Чем она ниже, тем более предпочтителен вариант (относительные расходы самые маленькие):
| Раздел 9. Анализ инвестиционной и инновационной деятельности |

Из расчетов следует, что второй вариант является более предпочтительным.
У предпринимателя всегда есть выбор, куда вложить свободные денежные средства. Такой выбор всегда является выбором того вида бизнеса, вложение средств в который принесет максимальный доход. При оценке целесообразности таких вложений исходят из того, явится ли такое вложение более прибыльным (при допустимом уровне риска), чем вложения в государственные ценные бумаги, или наоборот, т. е. анализируют будущие доходы при минимальном («безопасном») уровне доходности.
Для этого используют несложные математические методы, основная идея которых заключается в оценке будущих поступлений Рп (в виде прибыли, процентов, дивидендов) с позиции текущего момента.
Для этого используется формула:
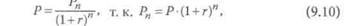
где Рп - доход, планируемый к получению в п-ш году;
Р - текущая (приведенная) стоимость (оценка величины дохода Рп с позиции текущего момента);
г - коэффициент дисконтирования.
То есть прогнозируемая величина Рп через п лет с позиции текущего момента будет меньшей и равной Р. Темп снижения прогнозной стоимости до текущего момента задается величиной знаменателя формулы, и прежде всего величиной процентной ставки. В этом случае коэффициент дисконтирования равен процентной ставке, устанавливаемой инвестором, т. е. тому относительному размеру дохода, который инвестор хочет или может получить на инвести-
Финансовый анализ
руемый им капитал. Определяя коэффициент дисконтирования, обычно исходят из так называемого безопасного, или гарантированного, уровня рентабельности финансовых инвестиций, который обеспечивается Национальным банком по вкладам или операциям с ценными бумагами.
К примеру, предприниматель имеет на счете в банке 40 тыс. грн. Банковский процент на вклад - 25% годовых. 11редприниматель получает предложение войти своим капиталом в организацию предприятия. Предоставленные предпринимателю расчеты показывают, что через 7 лет его капитал возрастет в 4 раза (Р„ = 4 40 = 160 тыс. грн).
Для того чтобы ответить на вопрос, следует ли согласиться с предложением, необходимо сравнить две суммы: получаемую в результате вложения в предприятие и в банковское учреждение. Первая сумма составляет 160 тыс. грн. Вторая рассчитывается по формуле:
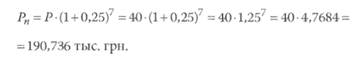
С предложением соглашаться не следует. Однако, даже в случае принятия положительного решения по результатам счета (т. е. если доход от вложения капитала выше дохода от вложения в банк), необходимо учесть фактор риска.
9.3. Анализ денежных потоков
при реализации инвестиционных проектов
В инвестиционном анализе важное место занимает оценка денежного потока, генерируемого в течение ряда временных периодов в результате реализации какого-либо проекта. Подобная оценка может выполняться в рамках решения двух задач:
♦ прямой (оценка с позиции будущего, когда реализуется схема наращивания);
♦ обратной (оценка с позиции настоящего, когда реализуется схема дисконтирования).
ч

|
Раздел 9. Анализ инвестиционной и инновационной деятельности
Финансовый анализ
текущую цену «на сегодня» всего денежного потока Рр Р2,..., Рпс позиции текущего момента. Как правило, расчеты денежных потоков ведутся по годовым данным.
К примеру, необходимо рассчитать величину приведенного денежного потока (с позиции текущего момента) в 20,25,15,35,40 тыс. грн, если коэффициент дисконтирования определен в 15% (табл. 9.1).
Таблица 9.1 Оценка приведенного денежного потока
| Показатель | Годы | Всего | ||||
| 1-й | 2-й | 3-Й | 4-й | 5-й | ||
| 1. Денежный поток (сумма возврата долга), тыс. грн | ||||||
| 2. Дисконтирующий множитель FM2(f.y при г = 15% (данные табличного табулирования) | 0,870 | 0,756 | 0,658 | 0,572 | 0,497 | |
| 3. Приведенный поток (сумма в долг с позиции текущего момента) стр. 1 х стр. 2, тыс. грн | 17,40 | 18,90 | 9,87 | 20,02 | 19,88 | 86,07 |
Денежный поток с равными поступлениями в течение ограниченного промежутка времени называется срочным аннуитетом. В этом случае поступления денежных потоков делаются в конце равных временных интервалов, на которые разбит данный промежуток времени (к примеру, регулярно поступающие рентные платежи за пользование сданными в аренду земельными участками).
Тогда
где А - величина аннуитета.
К примеру, если бы была возможность ежегодного получения аннуитета и дальнейшего его инвестирования на условиях банковского
Раздел 9. Анализ инвестиционной и инновационной деятельности
процента (или других условиях), то к концу четырехлетнего периода накопленная сумма может быть рассчитана по схеме:
♦ к концу первого периода будет получен аннуитет А;
♦ к концу второго года будет получен новый аннуитет А и приращение к нему в результате вложения полученной суммы аннуитета за первый период в банк под банковский процент, который составит процентную ставку г, т. е. А ■ (1+ г);
♦ к концу третьего года будет получен новый аннуитет и приращение к нему по результатам вложения суммы аннуитета с приращением конца второго периода в банк, т. е. А • (1+ r)-(l+ r) = (l+tf\
♦ к концу четвертого года будет получен новый аннуитет и приращение к нему по результатам вложения суммы аннуитета с приращениями конца третьего периода в банк, т. е. A-(l+r)2-(l+r) = (l+r)3.
Соответственно, в и-ный период времени сумма аннуитета с приращениями составит:
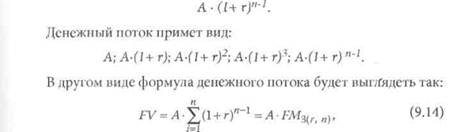
где FM3, и> - факторный множитель, смысл которого заключается в том, что он показывает, чему будет равна суммарная величина срочного аннуитета в одну денежную единицу (например, одна гривна) к концу срока его действия.
Предполагается, что производится лишь начисление денежных сумм, а их изъятие может быть сделано по окончании срока действия аннуитета.
Значения факторного множителя FM3(y n\ табулированы в специальных таблицах.
Финансовый анализ
К примеру, предпринимателю предложено инвестировать 100 тыс. грн на срок 5 лет при условии возврата этой суммы частями (ежегодно по 20 тыс. грн); по истечении пяти лет выплачивается дополнительное вознаграждение в размере 80 тыс. грн. Следует ли такое предложение принять, если у него есть «безопасная» возможность положить деньги на счет в банке из расчета 15% годовых?
Для принятия решения нужно сравнить две суммы: возвращенную из банка к концу пятилетнего периода и альтернативную сумму доходов от принятого предложения.
К концу пятилетнего периода возвращенная сумма из банка составит:

|
К концу пятилетнего периода альтернативная сумма доходов по результатам принятого предложения составит:
а) дополнительное вознаграждение - 80 тыс. грн;
б) денежный поток при заданных величинах регулярного поступ
ления (А) в сумме 20 тыс. грн и процентной ставке г = 15%
составит (FM^(r и,= 6,742 - из таблиц табулирования):

Таким образом, предложение нельзя считать целесообразным.
При решении обратной задачи срочного аннуитета (оценка будущих денежных поступлений с позиции текущего момента или текущей стоимости срочного аннуитета) используют (рассуждения такие же, как и при получении формулы (9.14), но при обратном денежном потоке или его дисконтировании) формулу:

Экономический смысл дисконтирующего множителя заключается в том, что он показывает, чему равна с позиции текущего момента
Раздел 9. Анализ инвестиционной и инновационной деятельности
величина аннуитета с регулярными денежными поступлениями в размере одной денежной единицы (например, гривни), продолжающегося п лет с заданной процентной ставкой г. Значения этого множителя также табулированы в специальных таблицах.
Бессрочный аннуитет - это денежный поток с равными поступлениями, продолжающийся достаточно длительное время (в практике инвестиционного анализа к бессрочным относятся аннуитеты, рассчитанные на 50 и более лет).
Прямая задача в этом случае не имеет смысла. Что касается обратной задачи, то ее решение возможно по формуле:

|
Такая формула чаще всего используется для оценки целесообразности приобретения аннуитета. В этом случае известен размер годовых поступлений, а в качестве коэффициента дисконтирования г обычно принимается гарантированная процентная ставка (к примеру, процент, предлагаемый государственным банком).
Определим текущую стоимость бессрочного аннуитета с ежегодным поступлением 600 тыс. грн, если банковский процент государственного банка составляет 11 %.

Можно сделать вывод, что если аннуитет предлагается по цене, не превышающей 5,45 млн грн, он представляет собой выгодную ин-
Финансовый анализ
вестицию, обеспечивающую больший денежный поток, чем поток средств от вложения денег в Национальный банк.
9.4. Анализ инвестиционных проектов
Анализ инвестиционных процессов, связанных с вложениями денежных средств в долгосрочные материальные и финансовые активы, представляет собой наиболее важный и сложный раздел финансового анализа. Принимаемые в этой области решения рассчитаны на длительные периоды времени и, как правило:
♦ являются частью стратегии развития фирмы в перспективе;
♦ влекут за собой значительные оттоки средств;
♦ с определенного момента времени могут стать необратимыми;
♦ опираются на прогнозные оценки будущих затрат и доходов.
Ключевым моментом при принятии инвестиционных решений яв
ляется оценка эффективности предполагаемых капиталовложений.
Совокупность методов, применяемых для оценки эффективности инвестиций, можно подразделить на две группы: динамические (основаны на дисконтированных оценках); статистические (учетные), основанные на учетных оценках срока окупаемости (см. рис. 9.2).

Рис. 9.2. Классификация методов инвестиционного анализа
Динамические методы отражают наиболее современные подходы к оценке эффективности инвестиционных проектов. Их часто называют дисконтными, так как они базируются на определении
Раздел 9. Анализ инвестиционной и инновационной деятельности
современной величины (или дисконтирования) денежных потоков, связанных с реализацией инвестиционного проекта.
При таком анализе обычно делаются следующие допущения:
♦ потоки денежных средств на конец (начало) каждого периода реализации проекта известны;
♦ определена оценка, выраженная в виде процентной ставки (нормы дисконта), в соответствии с которой средства могут быть вложены в данный проект. В качестве такой оценки обычно используются: средняя или предельная стоимость капитала для предприятия; процентные ставки по долгосрочным кредитам; требуемая норма доходности на вложенные средства и др.
В инвестиционном анализе в дальнейшем мы будем абстрагироваться от ее конкретного экономического содержания, используя термин «норма дисконта».
Поиск по сайту: