Частотные характеристики разомкнутых систем

Так как полиномы произвольного порядка можно разложить на простые множители, то любую передаточную функцию можно представить в виде произведений простых множителей в числителе и знаменателе или, другими словами, в виде цепочки последовательно соединенных типовых динамических звеньев. Для такой цепочки звеньев (т.е. для разомкнутой одноконтурной системы) передаточная и комплексная частотная функции запишутся в виде:

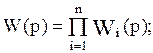
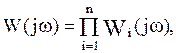
где 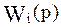и - передаточные и комплексные частотные функ-

ции типовых динамических звеньев.

В этом случае модули и аргументы комплексных функций звеньев и системы связываются следующими соотношениями:

.

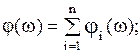
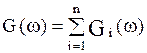Отсюда вытекает правило построения ЛАЧХ и ЛФЧХ разомкнутой одноконтурной САУ: строят логарифмические характеристики звеньев и затем их графически складывают.

Но для построения асимптотической ЛАЧХ применяют более простой метод, который сформулируем после рассмотрения численного примера.

Поиск по сайту: