 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Передаточная функция
Целью рассмотрения САУ может быть решение одной из двух задач: задачи анализа или задачи синтеза. Но в любом случае порядок исследования САУ включает в себя следующие этапы: математическое описание, исследование установившихся режимов, исследование переходных режимов.
Рассмотрим случай, когда в замкнутой системе можно выделить объект О и управляющее устройство УУ, как показано на рис.2.1.
 f(t)
f(t)
g(t) e(t) y(t) x(t)
УУ О
Рис.2.1
Общее уравнение САУ получается из системы уравнений объекта и управляющего устройства.
Состояние объекта характеризуется выходной величиной x(t), регулирующим воздействием y(t) и возмущением f(t). Тогда выходная величина может быть представлена функцией:

Состояние управляющего устройства характеризуется регулирующим воздействием y(t) и входным воздействием e(t). Процессы в УУ будут описываться двумя уравнениями:


Три последних уравнения полностью описывают процессы в САУ. Если в этих уравнениях исключить переменные y(t) и e(t), то получим дифференциальное уравнение САУ:

Это уравнение оценивает состояние системы во времени, определяет переходные процессы и обычно называется уравнением динамики.
Однако в форме дифференциальных уравнений математическое описание в теории автоматического управления обычно не применяется вследствие сложности решения таких уравнений.
Исследование САУ существенно упрощается при использовании прикладных математических методов операционного исчисления.
Возьмем некоторый элемент САУ, имеющий один вход и один выход. Дифференциальное уравнение элемента в общем случае имеет вид:
| (2.1) |

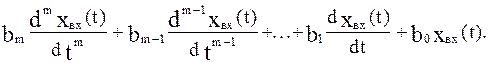
Если в уравнение (2.1) вместо функции времени  и
и  ввести функции
ввести функции 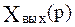 и
и  комплексного переменного р, поставив условием, что эти функции связаны зависимостями:
комплексного переменного р, поставив условием, что эти функции связаны зависимостями:
 (2.2)
(2.2)
то оказывается, что дифференциальное уравнение, содержащее функции  и
и  , при нулевых начальных условиях равносильно линейному алгебраическому уравнению, содержащему функции
, при нулевых начальных условиях равносильно линейному алгебраическому уравнению, содержащему функции 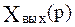 и
и  :
:

 (2.3)
(2.3)
Такой переход от дифференциального уравнения к однозначно соответствующему ему алгебраическому уравнению называется преобразованием Лапласа.
Функция  называется изображением функции
называется изображением функции  , функция
, функция  называется оригиналом функции
называется оригиналом функции  .
.
Операция перехода от искомой функции  к ее изображению
к ее изображению  (нахождение изображения от оригинала) называется прямым преобразованием Лапласа и записывается условно с помощью символа L как
(нахождение изображения от оригинала) называется прямым преобразованием Лапласа и записывается условно с помощью символа L как

Операция перехода от изображения  к искомой функции
к искомой функции  (нахождение оригинала по изображению) называется обратным преобразованием Лапласа и записывается условно с помощью символа
(нахождение оригинала по изображению) называется обратным преобразованием Лапласа и записывается условно с помощью символа  как
как
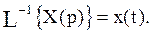
Формально переход от дифференциального уравнения к алгебраическому относительно изображения при нулевых начальных условиях получается путем замены символов дифференцирования оригиналов функций  ,
, 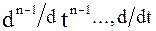 соответственно на
соответственно на  и функций
и функций  - их изображениями
- их изображениями  . С комплексной переменной
. С комплексной переменной  , как и с другими членами алгебраического уравнения, можно производить различные действия: умножение, деление, вынесение за скобки и т.д.
, как и с другими членами алгебраического уравнения, можно производить различные действия: умножение, деление, вынесение за скобки и т.д.
Так как возможность однозначного перехода от дифференциального уравнения к алгебраическому значительно упрощает расчеты, то важно убедиться в правомерности такого перехода.
Обозначим в исходном дифференциальном уравнении  и согласно интегралу (2.2) найдем изображение:
и согласно интегралу (2.2) найдем изображение:
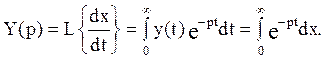
Согласно правилу интегрирования по частям


= 
При нулевых начальных условиях  и с учетом (2.2) получим:
и с учетом (2.2) получим:

Таким образом, операция дифференцирования оригинала соответствует операции умножения изображения этого оригинала на комплексное число  .
.
Так как
 то
то  и т.д.
и т.д.
Каждый элемент САУ в общем случае описывается дифференциальным уравнением вида (2.1). Следовательно, при выводе дифференциального уравнения системы в целом необходимо совместно решить несколько дифференциальных уравнений высших порядков.
Преобразование дифференциальных уравнений по Лапласу позволяет свести эту задачу к решению системы алгебраических уравнений. Определив из алгебраических уравнений изображение  искомой функции
искомой функции  , определяющей переходной процесс в системе, находят эту функцию, пользуясь таблицами оригиналов и изображений или по известным формулам обратного преобразования Лапласа.
, определяющей переходной процесс в системе, находят эту функцию, пользуясь таблицами оригиналов и изображений или по известным формулам обратного преобразования Лапласа.
Кроме того, преобразование дифференциального уравнения по Лапласу дает возможность ввести понятие передаточной функции.
Вынеся в уравнении (2.3)  и
и  за скобки, получим:
за скобки, получим:


Определим из этого уравнения отношение изображения выходной величины к изображению входной:
 (2.4)
(2.4)
Отношение изображения выходной величины элемента (или системы) к изображению его входной величины при нулевых начальных условиях называется передаточной функцией элемента (или системы).
Передаточная функция W(p) является дробно-рациональной функцией комплексной переменной р:

где  - полином степени n,
- полином степени n,
 - полином степени m.
- полином степени m.
Из определения передаточной функции следует, что:

Передаточная функция является основной формой математического описания объектов в теории автоматического управления и так как она полностью определяет динамические свойства объекта, то первоначальная задача расчета САУ сводится к определению передаточной функции.
Рассмотрим примеры по определению передаточной функций некоторых простейших схем, характерных для электроники.
Поиск по сайту: