 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Пример 3.4
Для САУ, структурная схема которой приведена на рис.3.3, определить область устойчивости методом D- разбиения. Варьируемые параметры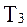 
и 
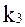. Значения неварьируемых параметров:
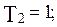
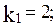
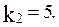
Характеристический полином замкнутой САУ:
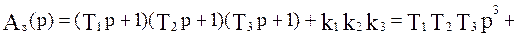
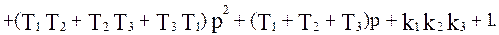
Представим последнее выражение в следующем виде:
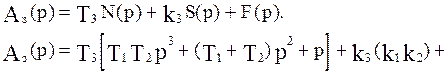
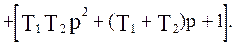
Сделаем подстановку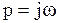 
:
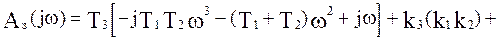
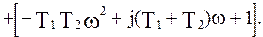
Выделим вещественную и мнимую части, представив их в следующем виде:
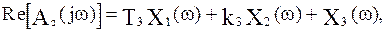
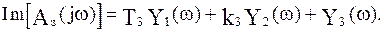
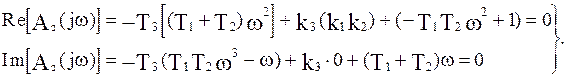
Рассчитаем для последней системы уравнений определител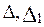и 
и 
:
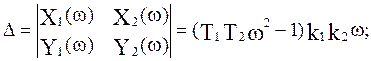
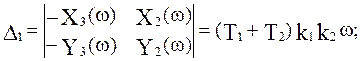
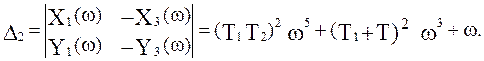
Найдем выражения для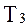 
и :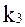
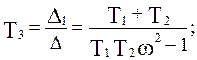
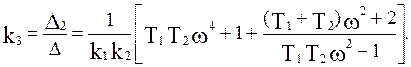
Подставляя численные значения, получим:
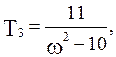
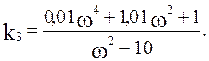
Результаты расчетов границы области устойчивости по последним выражениям сведены в таблицу. Еще две границы получаются в результате приравнивания нулю коэффициента характеристического полинома при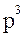 
(
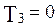) и свободного члена характеристического полинома:
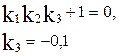
Область устойчивости построена на рис.3.9.
Таблица
| w | ||||||||||
| Т3 | -1,1 | -1,2 | -1,83 | -11 | 1,83 | 0,73 | 0,28 | 0,12 | 0,051 | 0,028 |
| k3 | -0,1 | -0,22 | -0,86 | -10,9 | 3,29 | 2,17 | 1,91 | 2,24 | 3,42 | 5,14 |
k3
w=10 w=4
2 w=7 w=5
Область
1 устойчивости
-1 0
Т3
1 2
w=1 -1
w=2
Рис.3.9
Поиск по сайту: