Арифметичні схеми

Перейдемо від СІС загального призначення до комбінаційних схем СІС, що використовуються для виконання арифметичних операцій.

Схеми зсуву. Першою із арифметичних схем СІС розглянемо схему зсуву, що містить 8 входів і 8 виходів (рис. 4.15). Вісім вхідних бітів подаються на лінії D₀,..., D₇. Вихідні дані, що представляють собою вхідні дані, зміщені на 1 біт, надходять на лінії S₀,..., S₇. Лінія керування С визначає напрямок зсуву: 0 – ліворуч, 1 – праворуч.

Рис. 4.15 - Схема зсуву

Щоб зрозуміти, як працює така схема, розглянемо пари вентилів І (крім крайніх вентилів). Якщо С=1, правий член кожної пари включається, пропускаючи через себе відповідний біт. Так як правий вентиль І з'єднаний із входом вентиля АБО, що розташований праворуч від цього вентиля І, відбувається зсув вправо. Якщо С=0, включається лівий вентиль І з пари, і тоді відбувається зсув вліво.

Суматори. Схема для виконання операцій додавання є істотною частиною будь-якого процесора. Таблиця істинності для додавання однорозрядних цілих чисел показана на рис. 4.16 а. Тут приведені два результати: сума вхідних змінних А і В і перенос на наступну (ліву) позицію. Схема для обчислення біта суми і біту переносу показана на рис. 4.16 б. Така схема, як правило, називається напівсуматором.

а) б)

Рис. 4.16 - Таблиця істинності для додавання однорозрядних чисел (а); схема напівсуматора (б)

Напівсуматор підходить для додавання бітів нижніх розрядів двох багатобітових слів. Але він не придатний для додавання бітів у середині слова, тому що не може здійснювати перенос у цю позицію. Тому потрібний повний суматор (рис. 4.17). Зі схеми повинно бути ясно, що повний суматор складається з двох напівсуматорів. Сума дорівнює 1, якщо непарне число змінних А, В і Вхід переносу приймає значення 1 (тобто якщо одиниці дорівнює або одна зі змінних, або всі три). Вихід переносу приймає значення 1, якщо або А і В одночасно рівні 1 (лівий вхід у вентиль АБО), або якщо один з них дорівнює 1, а Вхід переносу також дорівнює 1. Два напівсуматора породжують і біти суми, і біти переносу.

Щоб побудувати суматор, наприклад, для двох 16-бітних слів, потрібно продублювати схему, зображену на рис. 4.17 б, 16 разів. Перенос здійснюється в лівий сусідній біт. Перенос у самий правий біт з'єднаний з 0. Такий суматор називається суматором з наскрізним переносом. Додавання 1 до числа 111...111 не здійсниться доти, поки перенос не пройде весь шлях від самого правого біта до самого лівого. Існують більш швидкі суматори, що працюють без подібної затримки. Природно, перевага віддається їм.

Розглянемо приклад більш швидкого суматора. Розіб'ємо 32-розрядний суматор на 2 половини: нижню 16-розрядну і верхню 16-розрядну. Коли починається додавання, верхній суматор ще не може приступити до роботи, оскільки він не знає значення переносу, поки не завершиться 16 сумування у нижньому суматорі.

Однак можна зробити одне перетворення. Замість одного верхнього суматора можна одержати два верхніх суматора, продублювавши відповідні частини апаратного забезпечення. Тоді схема буде складатися з трьох 16-розрядних суматорів: одного нижнього і двох верхніх U0 і U1, що працюють паралельно. У суматор U0 в якості переносу надходить 0, а в суматор U1 в якості переносу надходить 1. Обидва верхніх суматора починають роботу одночасно з нижнім суматором, але тільки один з результатів сумування в двох верхніх суматорах буде правильним. Після додавання 16 нижніх розрядів стає відоме значення переносу у верхньому суматорі, і тоді можна визначити правильну відповідь. При такому підході час додавання скорочується в два рази. Такий суматор називається суматором з вибором переносу. Можна розбити кожний 16-розрядний суматор на два 8-розрядних і т.д.

Арифметико-логічні пристрої. Більшість комп'ютерів містять одну схему для виконання операцій І, АБО і додавання над двома машинними словами. Звичайно така схема для n-бітних слів складається з п ідентичних схем для індивідуальних бітових позицій. На рис. 4.18 зображена така схема, що називається арифметико-логічним пристроєм, або АЛП. Цей пристрій може обчислювати одну з 4 наступних функцій: А І В, А АБО В, 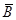і А+В. Вибір на лінії F₀ і F₁: 00,01,10 або 11 (у двійковій системі числення). Відзначимо, що тут А+В означає арифметичну суму А і В, а не логічну операцію І.

У лівому нижньому куті схеми знаходиться двохрозрядний декодер, який породжує сигнали включення для чотирьох операцій. Вибір операції визначається сигналами керування F₀ і F₁. В залежності від значень F₀ і F₁ вибирається одна з чотирьох ліній дозволу, і тоді вихідний сигнал обраної функції проходить через останній вентиль АБО.

а) б)

Рис. 4.17 - Таблиця істинності для повного суматора (а); схема для повного суматора (б)

Рис. 4.18 - Однорозрядний АЛП

У верхньому лівому куті схеми знаходиться логічний пристрій для обчислення А І В, А АБО В і 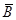, але принаймні один з цих результатів проходить через останній вентиль АБО в залежності від того, яку з ліній дозволу, вибрав декодер. Так як рівно один з вихідних сигналів декодера буде дорівнює 1, то і запускатися буде рівно один з чотирьох вентилів І. Інші три вентилі будуть видавати 0 незалежно від значень А і В.

АЛП може виконувати не тільки логічні й арифметичні операції над А і В, але і робити їх рівними нулю, заперечуючи ENA (сигнал дозволу А) або ENB (сигнал дозволу В). Можна також одержати 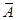, встановивши INVA (інверсію А). При нормальних умовах і ENA, і ENB рівні 1, щоб дозволити надходження обох вхідних сигналів, а сигнал INVA дорівнює 0. У цьому випадку А і В просто надходять у логічний пристрій без змін.

Рис. 4.19 - Вісім однорозрядних секцій, з'єднаних у 8-розрядний АЛП. (Сигнали дозволу й інверсії не показані для спрощення схеми)

У нижньому правому куті знаходиться повний суматор для підрахунку суми А і В і для здійснення переносів. Переноси необхідні, оскільки кілька таких схем можуть бути з'єднані для виконання операцій над цілими словами. Однорозрядні схеми, подібні тій, яка зображена на рис. 4.18, називаються розрядними мікропроцесорними секціями. Вони дозволяють розробнику сконструювати АЛП будь-якої бажаної ширини. На рис. 4.19 показана схема 8-розрядного АЛП, побудованого з восьми однорозрядних секцій. Сигнал INC (збільшення на одиницю) потрібний тільки для операцій додавання. Він дає можливість обчислювати такі суми, як А+1 і А+В+1.

Поиск по сайту: