 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Единицы стоимость единицы
капитала К2 единицы капитала К2 капитала К2
то есть когда
. (18)
Действительно, из (17) видно, что 
(богатство при увеличении инвестиций растет), когда 
, то есть, когда отдача от дополнительной единицы капитала, получаемой в результате инвестиций больше, чем затраты использования капитала. Богатство падает при увеличении инвестиций, когда 
, то есть, когда отдача от дополнительной единицы капитала, получаемой в результате инвестиций меньше, чем затраты использования капитала.
Определив количество инвестиций, максимизирующих его богатство, домохозяйство решает стандартную задачу потребительского выбора при новом уровне богатства, определяя уровень текущего и будущего потребления.
Решение об оптимальном количестве капитала фирмы, арендующей капитал. Предположим, что фирма не является владельцем капитала, она его арендует. Тогда объем капитала будет определяться фирмой из условия максимизации прибыли. Если мы предполагаем, что фирма существует не один период времени, то в этом случае она будет максимизировать поток прибыли, который получит в течение периода ее существования.
Рассмотрим поведение фирмы в этом случае с помощью двухпериодной модели. Если норма амортизации не равна нулю, и фирма арендует капитал, то издержки фирмы на единицу капитала в каждом периоде будут определяться ставкой процента и нормой амортизации, тогда прибыль фирмы в первом и во втором периоде в этом случае может быть определена с помощью следующей системы уравнений
Таким образом, в рамках двухпериодной модели межвременного выбора, фирма, арендующая капитал, будет решать следующую задачу условной оптимизации
,
при условии, что
Составим для этой задачи функцию Лагранжа
,
и запишем для этой функции условия оптимизации первого порядка для выпуска и капитала
,
(19)
.
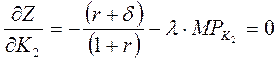Из (19) мы можем найти условие оптимального запаса капитала для фирмы, арендующей капитал, оно имеет следующий вид
MPK = r + d.
Как мы видим, условие оптимального запаса капитала для фирмы, арендующей капитал, совпадает с условием (18), условием выбора количества капитала, оптимизирующего богатство домохозяйства, в случае, когда капитал принадлежит фирме, и финансирование инвестиций производится за счет дополнительного выпуска акций.
Таким образом, значение оптимального запаса капитала не зависит, при прочих равных условиях, от того какая фирма определяет оптимальный уровень этого значения, фирма владеющая капиталом или фирма, арендующая капитал.
Поиск по сайту: