ИЗДЕРЖЕК ПРИСПОСОБЛЕНИЯ

Рассмотрев вышеизложенные модели инвестирования, можно сделать вывод о том, что существуют две основные причины, побуждающие фирму инвестировать. Первая, состоит в желании фирмы достичь оптимального с ее точки зрения количества капитала. Вторая, состоит в желании получить выгоду от разницы между стоимостью фирмы на фондовом рынке и стоимостью капитальных благ, которыми владеет предприятие. Если бы фирмы могли мгновенно реализовывать свои желания, то они всегда бы имели оптимальный запас капитала, и коэффициент q всегда бы был равен единице. Одной из причин того, что фирма не может мгновенно перейти к оптимальному для нее количеству капитала, служат так называемые издержки приспособления (adjustment cost).

Издержки приспособления (adjustment cost) – это издержки, которые несет фирма при изменении объема основного капитала.

В основе издержек приспособления лежат издержки на установку нового капитала. Они возникают, когда у фирмы возникает как недостаток, так и избыток капитала. Затраты на установку (J) являются функцией от уровня инвестиций J=J(I), причем , то есть увеличение инвестиций приводит к ускоренному росту издержек установки.

Кроме того, в отличие от процентной ставки и нормы амортизации, характеризующих постоянные затраты, затраты на установку носят временный характер. После того как оборудование будет введено, они будут равны нулю, то есть J (0)=0 и .

Введение издержек установки меняет условие выбора оптимального количества капитала, так как появляются дополнительные затраты, и теперь, при той же процентной ставке и той же норме амортизации, требуется больший предельный продукт капитала, чтобы покрыть соответствующие общие затраты. Получить данный вывод можно с помощью задачи максимизации прибыли фирмой, введя в нее издержки приспособления.

Двухпериодная модель межвременного выбора с учетом издержек приспособления. Рассмотрим поведение фирмы, которая существует только два периода. Будем для определенности считать, что фирма является собственником капитала, в конце второго периода продает капитал по остаточной стоимости, и что инвестиции финансирует за счет своих сбережений, то есть, из нераспределенной прибыли, кроме того, инвестиции сопровождаются издержки приспособления. Тогда прибыль, которую получит фирма в первом и втором периоде определяется следующим образом

Допустим, что, действуя как рациональный агент, фирма будет принимать решение о количестве необходимых ей инвестиций, максимизирую поток прибыли, который она получит в течение периода ее существования, то есть,

,

при условии, что

Тогда функция Лагранжа имеет следующий вид

.

Запишем для данной функции Лагранжа условия первого порядка для инвестиций и капитала

, (30)

. (31)

Из (30), (31) следует, что условие оптимального запаса капитала в данном случае имеет следующий вид

MP_K=r+d+ .

Когда l=1, тоданное условие превращается в условие оптимального запаса капитала, полученное ранее в модели не учитывающей издержки приспособления. В то же время из (30) следует, что условие l=1 может выполняться только в том случае, если нет издержек приспособления, то есть, если инвестиции отсутствуют. В других случаях из-за издержек приспособления l не равняется единице.

Допустим, что l >1, тогда из (31) следует, что в этом случае MP_K>(r + d). Следовательно, затраты на дополнительную единицу капитала в этом случае меньше, чем выгода от нее. Поэтому единичное изменение стоимости имеющего у фирмы капитала приведет к росту ее стоимости на фондовом рынке, то есть к росту стоимости ее акций больше чем на единицу. В этом случае вложения в капитал данной фирмы целесообразны, надо увеличивать инвестиции в эту фирму.

Если l < 1, то MP_K <(r + d). Это означает, что затраты на дополнительную единицу капитала больше, чем выгода от нее. Следовательно, изменение стоимости имеющего у фирмы капитала приведет к росту ее стоимости на фондовом рынке, то есть к росту стоимости ее акций меньше чем на единицу. Поэтому, для достижения оптимального уровня, предельный продукт капитала надо увеличивать, а капитал сокращать. То есть, инвестиции в данный капитал нецелесообразны.

Поведению множителя Лагранжа как мы видим схоже с поведением коэффициента q-Тобина. Это обусловлено тем, что множитель Лагранжа оценивает, как изменение условия воздействует на изменение целевой функции. То есть, множитель Лагранжа в данном случае оценивает, как изменение стоимости капитала воздействует на изменение рыночной стоимости фирмы. Таким образом, действительно в предельном случае, множитель Лагранжа является коэффициентом q-Тобина.

Проанализируем теперь поведение фирмы, период жизни которой неограничен. Предположим, что период жизни фирмы неограничен. Для простоты анализа предположим, что норма амортизации равна нулю. В этом случае прибыль фирмы за период (t+i) можно представить в следующем виде

(32)

Если предположить, что рационально действующая фирма максимизирует прибыль, которую она может получить, то находясь в периоде t, фирма принимает решение об инвестициях таким образом, чтобы поток будущих прибылей приведенный к настоящему моменту (V_t) был максимальным, то есть,

max .

При ограничении (32) запишем функцию Лагранжа для нашей задачи условной оптимизации

.

Если ввести, что

,

то можно привести функцию Лагранжа к следующему виду

(33)

Из (33) следует, чтозначение величины q_t+i можно интерпретировать как теневую цену единицы капитала в период (t+i) если фирма ведет себя оптимальным образом. В предельном случае величина q_t+i является коэффициентом q-Тобина для периода (t+i).

Выпишем необходимое условие оптимума первого порядка для I_t+i и K_t+i (i=1, 2,…)

, (34)

. (35)

Из (35) можно найти условие оптимального запаса капитала для периода (t+i), где i=1,2,…

,

которое можно преобразовать, обозначив

,

в следующее условие

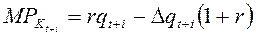. (36)

Из (36) выразим q_t+i

. (37)

Если , то есть, ценность единицы капитала с течением времени растет, то капитал увеличивать целесообразно. Если , то есть, ценность единицы капитала с течением времени падает, то капитал увеличивать нецелесообразно. Следовательно, капитал не надо изменять в случае, когда , то есть ценность единицы капитала с течением времени не изменяется.

Если , то капитал в экономике растет, то есть, инвестиции в экономике увеличиваются. Если , то капитал в экономике падает, то есть, инвестиции в экономике уменьшаются. Если , то капитал в экономике остается неизменным, инвестиции не требуются.

Выражения (34) и (37) позволяют найти условия оптимального запаса капитала и уровня инвестиций для периода (t+i) если

,

то

.

Таким образом, в случае, когда период жизни фирмы не ограничен, решение об инвестициях принимается не только на основе предельной выгоды и предельных затрат от единицы капитала, инвестируемой в какой-то период (t+i), но также на основе изменения теневой цены капитала, которая и определяет целесообразность инвестиционных вложений в капитал.

Динамика модели. Проанализируем динамику модели инвестиций с учетом издержек приспособления, используя фазовую диаграмму.

Опишем сначала стационарное состояние экономики, которое для нашей модели характеризуется условиями .

Рис. 8.

Допустим сначала, что , тогда из (37) следует, что в этом случае 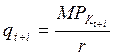, если , то , если , то . Следовательно, на рис.8 для точек, лежащих на графике теневая цена единицы капитала в период (t+i) остается постоянной. Для точек, лежащих выше этого графика происходит увеличение теневой цены капитала в период (t+i) по сравнению с предыдущим периодом. Для точек, лежащих ниже этого графика происходит уменьшение теневой цены капитала в период (t+i) по сравнению с предыдущим периодом.

Рис.9.

Допустим теперь, что уровень капитала с течением времени не изменяется, то есть, . Так как это означает, что инвестиционных вложений в период (t+i) нет, то из (34) следует, что . То есть, для точек лежащих на линии (рис.9), изменение капитала не происходит. Если , то из (34) следует, что . То есть, в точках, лежащих выше линии , капитал растет (рис.9). Если , то из (34) следует, что , следовательно, в точках, лежащих ниже этой линии капитал снижается (рис.9).

Совместив два графика (рис.8 и рис.9), мы получим фазовую диаграмму, которая позволит проанализировать динамическое поведение экономики из любой первоначальной точки (рис.10).

Рис. 10.

Как видно на рис.10 пространство координат разделилось на четыре сектора, в которых результат динамического поведения экономики будет различным. Если первоначально экономика будет находиться в секторах II и IV, то с течением времени экономика придет в состояние равновесия

.

Если же экономика первоначально будет находиться в секторах I и III, то с течением времени экономика не только не придет в состояние равновесия, напротив она будет отдаляться все дальше и дальше от состояния равновесия.

Если экономика первоначально будет находиться в первом и третьем секторе, то под воздействием динамики К и q она будет удаляться от состояния равновесия. Если экономика первоначально будет находиться во втором или четвертом секторе, то под воздействием динамики К и q она будет стремится к состоянию равновесия.

Влияние экзогенных параметров на состояние равновесия. Исследуем, как внешние по отношению к модели инвестиций с учетом издержек приспособления факторы влияют на равновесное состояние экономики в этой модели.

Предположим, что в экономике, находившейся ранее в состоянии равновесия, произошло увеличение выпуска за счет увеличение труда. В этом случае,так как предельный продукт капитала вырастет при том же уровне капитала, произойдет сдвиг графика вверх и вправо.Новому состоянию равновесия будет соответствовать более высокий уровень капитала (К**>K*). Следовательно, инвестиции в этом случае возрастут.