 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Вязко-упругое тело Кельвина
|
Читайте также: |
График течения

| т | ||
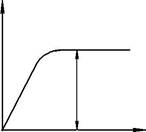
Вязко-упругое тело Кельвина представляет собой механическую модель, полученную при параллельном соединении упругого элемента Гука с модулем упругости G и вязкого элемента Ньютона с вязкостью µ.
Модель Вид модели График течения



| Вязко- | |||||||||||||||||||||||||||
| упругое | |||||||||||||||||||||||||||
| тело | G | µ | |||||||||||||||||||||||||
| Кельвина | |||||||||||||||||||||||||||





| 0 | |||
| t1 | t | ||
| 0 | |||
| 1 | |||
| t1 | t |
Под действием растягивающего усилия пружина удлиняется, а поршень в этот момент будет двигаться, это движение связано с возникновением сопротивления жидкости в виду чего полное растяжение пружины наступает не сразу. Когда нагрузка устранена пружина сжимается до первоначальной длины, но на это требуется определенное время вследствие вязкого сопротивления в поршне.
Для описания модели тела Кельвина примем во внимание то обстоятельство, что при параллельном соединении элементов, деформация сложного тела γк будет равна деформации каждого элемента
γк=γг=γн
а напряжение сложного тела τ будет равно сумме напряжений в отдельных элементах Гука и Ньютона.
τк=τг+τн
| г | G г | |||
| н | ||||
| н |
Рассмотрев совместно 2 системы этих уравнений, получим окончательную модель для тела Кельвина.
G г н
Где τ – касательное напряжение, Па G – модуль упругости при сдвиге, Па γ – угловая деформация µ – динамическая вязкость, па∙с – скорость сдвига с-1
Кельвин ввел идеальное тело для того, чтобы иметь возможность показать свойства вязкого течения твердого тела.
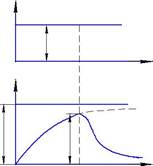
Для тела Кельвина характерно явление ползучести.
Ползучесть –это нарастание во времени деформации при постоянномзначении приложенных напряжений.
Решив реологическое уравнение тела Кельвина при 0 const получим ур-ние
G
0 Ce t

 G
G
где t – время, с.
Постоянная интегрирования С определяется из начальных условий т.е. при t=0; 0 0, тогда
C 0
 G
G
Подставим значение С в уравнение получим окончательное уравнение которое называется уравнение ползучести
| G | t | |||||||||||||||
| 1 e | ||||||||||||||||
| G | ||||||||||||||||
Поиск по сайту: