 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Квантовое состояние и вырождение
| 112 211 121 |
| 122 212 221 |
| 113 311 131 |
| Рис. 1.5. Энергетические уровни частицы в трехмерном потенциальном ящике |

|

|

|
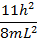
|
Схема энергетических уровней частицы, движущейся в трехмерном потенциальном ящике, более сложная, чем аналогичная схема для частицы, движущейся в одномерном потенциальном ящике. Эта схема представлена на рис. 1.5, где использован ряд обозначений. Для обозначения Ψ-функции используются квантовые числа, связанные с этой волновой функцией. Следовательно, Ψ-функция для частного набора квантовых чисел n1, n2, n3 записывается в виде Ψ(n1, n2, n3). Она является одним из линейно независимых решений дифференциального уравнения. Эта функция характеризует возможное состояние системы, физически отличное от всех других состояний или функций. Термин «квантовое состояние» используется для обозначения состояния системы, описываемого частным линейно независимым решением уравнения Шредингера, определяемым соответствующим набором квантовых чисел.
На рис. 1.5 обнаруживается явление, характерное для трехмерных задач. Можно показать, что для энергии данный энергетический уровень может быть получен путем задания нескольких комбинаций квантовых чисел. Например, второй энергетический уровень соответствует квантовым состояниям (112), (121) или (211). Указанные Ψ-функuии и, следовательно, связанные с ними квантовые состояния в действительности отличаются друг от друга, как это можно увидеть, если записать Ψ-функции в явном виде:
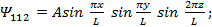
 (1.31)
(1.31)

В квантовом состоянии (112) частица движется, «прыгает» туда и обратно в направлении zс импульсом, вдвое большим, чем в направлениях х и у. В состоянии (121) частица обладает импульсом в направлении y, вдвое большим, чем в направлениях х и zи т. д. Однако главным является то обстоятельство, что указанные три квантовых состояния обладают одной и той же энергией.
Если какой-нибудь энергетический уровень соответствует не одному, а нескольким квантовым состояниям, то этот энергетический уровень называется вырожденным.Рассмотренный нами выше энергетический уровень является трижды вырожденным, так как он может быть реализован тремя различными способами. Наинизший энергетический уровень (см. рис. 1.5) не вырожден, так как он осуществляется только при единственном наборе квантовых чисел.
Поиск по сайту: