 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Решетки Браве
| Рисунок 1.8. Различные способы выбора элементарной ячейки для двухмерной решетки |
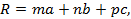(1.42)
где m, n, p- числа, которые обычно выражают в долях ребер ячейки и называют индексами данного узла.
Совокупность трех индексов обычно записывают в двойных квадратных скобках [[mnp]]и называют символом узла.Элементарная ячейка в общем случае представляет собой косоугольный параллелепипед с ребрами a, b, c и углами α (=bc), β (=ca), γ (=ab)(рис. 1.9). Шесть указанных величин называются параметрами решетки.Параметры a, bи с, определяющие размер элементарной ячейки, называются постоянными решетки.
| z |
| y |
| x |
| c |
| b |
| a |
| γ |
| β |
| α |
| Рисунок 1.9. Элементарная ячейка |
Существуют еще и сложные ячейки: объемно-центрированная ячейка, в которой дополнительный узел лежит на пересечении телесных диагоналей; базоцентрированная ячейка, у которой центрировано основание; бокоцентрированная ячейка, которых может быть две (когда центрирована грань, перпендикулярная оси а, и когда центрирована грань, перпендикулярная оси b; гранецентрированная ячейка, в которой дополнительные узлы находятся в центре граней.
Идеальный монокристалл представляет собой бесконечное повторение в трехмерном пространстве идентичных блоков одинаковой ориентации. Каждый блок, называемый базисом, может представлять собой атом, молекулу либо группу атомов или молекул. Базис - это количество вещества, содержащегося в элементарной ячейке, которая имеет форму трехмерного параллелепипеда. Перемещая этот параллелепипед на определенные дискретные расстояния во всех трех направлениях, можно заполнить все пространство. Трансляционная симметрия является наиболее очевидной для кристаллических твердых тел. Множество операторов трансляции определяют пространственную решетку, или решетку Браве. В кристаллографии для аналитического описания кристаллов пользуются трехмерной системой координат, которую выбирают в соответствии с симметрией кристалла.
Оси координат, как правило, совпадают с ребрами элементарной ячейки, причем их выбирают таким образом, чтобы они совпадали с особыми, прежде всего с главными особыми (одиночными для данного кристалла), направлениями решетки и были равны кратчайшим трансляциям в этих направлениях. Особыми направлениями являются оси симметрии или нормали к плоскостям симметрии. Если особых направлений нет, то ребра ячейки выбирают по рядам кристаллической решетки или по ребрам кристаллического многогранника.
При таком выборе элементарных ячеек все кристаллы можно объединить в шесть кристаллографических систем координат, или сингоний (табл. 1.1). В каждой сингонии объединяются те кристаллы, для которых одинакова симметрия элементарных ячеек, их структур и одинакова система осей координат. В 1848 г. О. Браве удалось математическим путем доказать, что существует всего 14 типов трансляционных решеток, отличающихся по своей симметрии. О. Браве сформулировал три условия, последовательное выполнение которых позволяет из бесчисленного множества элементарных ячеек выбрать одну определенную, характеризующую всю решетку в целом:
Таблица 1.1 Сингонии и правила кристаллографической установки
| Сингония | Характеристики элементарной ячейки | Принятые правила расположения осей |
| Триклинная | 
| По ребрам кристалла,
|
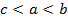
| Моноклинная | 
| Ось у вдоль оси 2 или вдоль нормали к плоскости m |
| Ромбическая | 
| Оси х, у, z вдоль трех взаимно- перпендикулярных осей 2 или вдоль нормалей к плоскостям m |
| Тетрагональная | 
| Ось 4 - ось z. Остальные - в плоскости ху |
| Гексагональная | 
| Ось 6 (ось 3 в тригональной сингонии) |
| Кубическая | 
| Оси х, у, z параллельны трем взаимно-перпендикулярным осям 4 или 2 |
1) сингония выбранной ячейки должна быть такой же, как и сингония всей решетки, т. е. симметрия должна соответствовать симметрии всей решетки (симметрия ячейки должна максимально совпадать с точечной симметрией кристалла);
2) число прямых углов и равных сторон должно быть максимальным;
3) при соблюдении первых двух условий объем ячейки должен быть минимальным.
Таким образом, при стандартном выборе элементарной ячейки в соответствии с внешней симметрией кристалла и соблюдении условий Браве любая кристаллическая структура может быть представлена с помощью одной из 14 топологических решеток Браве.
Среди этих 14 решеток только шесть (с учетом примитивной ромбоэдрической ячейки - семь) являются примитивными, по которым и различают кристаллографические сингонии. Оставшиеся восемь решеток имеют дополнительные узлы, т. е. такие решетки являются центрированными. Таких дополнительных узлов может быть только один, два или три, и они располагаются либо в объеме решетки, либо в гранях.
Поиск по сайту: