 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Энергия Ферми
В металле энергия наивысшего уровня Еfявляется отрицательной величиной, как это следует из рис. 1.6. Трансляционная часть этой энергии, обозначенная εf - положительная величина, поскольку она отсчитывается от дна зоны Еатомн. Будем называть энергию εf кинетической энергией Ферми.
Различные трансляционные энергетические уровни простейших металлов удается описать, используя элементарные положения квантовой механики. Существует трансляционный импульс ртранс, соответствующий трансляционному движению. Трансляционнaя энергия и импульс связаны следующим соотношением:
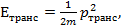(1.33)
где m - масса электрона.
Энергия является периодической функцией импульса и может быть аппроксимирована квадратичной функцией только для состояний, лежащих около дна зоны. Использование соотношения (1.33) допустимо, когда электроны заполняют только часть зоны.
Зона в целом состоит из Ngуровней. Следовательно, уровни энергии представляют собой дискретный, но плотно упакованный набор. Чтобы каждое из дискретных трансляционных состояний можно было отличить от всех остальных, эти состояния должны отличаться друг от друга по импульсу на величину, определяемую принципом неопределенности.
Рассмотрим конкретно составляющую импульса по оси х. Неопределенность положения любого электрона в твердом теле ∆х равна размеру L кристалла в направлении оси х. Принцип неопределенности для х-компонент импульса и координаты запишется в виде
(1.34)
где предполагается, что неопределенность в измерении pxявляется минимальной. Если соотношение (1.34) дает минимальное значение неопределенности в измерении импульса произвольного состояния, то в случае, когда импульсы всех других состояний не отличаются от импульса рассматриваемого состояния на величины, превышающие значение неопределенности 
, эти состояния не являются дискретными и их нельзя отличить друг от друга.
Реальный кристалл является трехмерным, и значение неопределенности в измерении импульса в направлении каждой координатной оси равно h/L (для куба с ребром L). Тогда неопределенность в измерении импульса каждого состояния представляет собой не одномерную величину, а трехмерную в пространстве импульсов. Минимальное значение объема в трехмерном импульсном пространстве, характеризующее неопределенность импульса, равно:
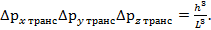(1.35)
| pf |
| pz |
| Рис 1.7. Один октант сферы Ферми в пространстве импульсов |
| px |
| py |
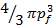, а элементарный объем, соответствующий каждому состоянию в пространстве импульсов, равен hЗ /L3. Так как в каждом состоянии с данным импульсом находятся два электрона: один со спином, ориентированным вверх, другой со спином, ориентированным вниз, полное число состояний в пространстве импульсов, занимаемым N электронами, равно N/2.Это число должно равняться частному от деления полного объема сферы на элементарный объем h3/ L3:
(1.36)
В выражении (1.36) не содержится в явном виде кинетическая энергия Ферми εf, но величина pfсвязана с кинетической энергией Ферми соотношением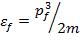 
Следовательно, выражение (1.36) можно записать в виде
(1.37)
С другой стороны, εf можно выразить через полное число электронов:
(1.38)
Кинетическая энергия Ферми, таким образом, зависит лишь от числа электронов в единице объема 
.
Кинетическая энергия Ферми, определяемая выражением (1.38), представляет собой наибольшую трансляционную энергию электронов у верхней границы данного распределения и, следовательно, позволяет количественно определить ширину зоны через число электронов в ней. Величина εf для простейших металлов с одним s-электроном, щелочных металлов и других составляет примерно 3... 5 эВ.
Представление сферы Ферми в виде гладкой поверхности сомнительно, поскольку объем каждого состояния в пространстве импульсов имеет форму куба; следует скорее считать поверхность Ферми не гладкой, а имеющей своеобразную мелкозернистую структуру. Однако степень зернистости этой структуры очень незначительна: энергия εf составляет 5 эВ, тогда как pf- порядка 10-24 кг·м/с. Таким образом, зернистость структуры поверхности Ферми практически ничтожна.
Описанная картина энергетической зоны применима только для зон, описывающих состояния s-электронов. Расчет энергии Ферми для более высоких состояний требует учета исходного вырождения этих состояний. Например, р-состояниесвободного атома состоит из шести вырожденных состояний. Эти трансляционные состояния согласно принципу Паули не отличаются друг от друга по энергиям. Следовательно, в выражении (1.38), содержащем в явной форме множитель 2 для s-зоны, этот множитель в случае р- и d-зон необходимо заменить более подходящим. Выражения (1.37) и (1.38) в общем виде следует представить следующим образом:
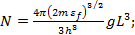(1.39)
, (1.40)
где g- степень вырождения атомных уровней в простых зонах.
Поиск по сайту: