Релаксационные переходы

Переход системы частиц в состояние термодинамического равновесия называется процессом релаксации, а квaнтoвыe переходы, которые способствуют установлению и поддержанию тер­модинамического равновесия, называются релаксационными переходами. В качестве примера, иллюстрирующего релаксационные переходы, рассмотрим процессы в некотором объеме га­за. Как известно, молекулы газа находятся в тепловом хаотическом движении, причем сред­няя кинетическая энергия молекулы газа пpoпорциональна kT (k - постоянная Больцмана; Т - абсолютная температура газа). В процессе теплового хаотического движения молекулы газа сталкиваются между собой. При этом сталкивающиеся частицы могут взаимодейство­вать между собой либо упруго, т.е. без изменения суммарной кинетической энергии стaлки­вающихся частиц, либо неупруго, когда часть кинетической энергии одной частицы может перейти во внyтpeннюю энергию другой (или наоборот: внутренняя энергия одной частицы может перейти в кинетическую энергию другой). В состоянии термодинамического (тепло­вого) равновесия температура газа и суммарная кинетическая энергия всех частиц остаются неизменными. Неизменна и внутренняя энергия частиц, которая распределяется между уровнями по закону Больцмана.

Если нарушить равновесие, например, резко увеличить температуру газа до величины Т₂, то при новой температуре средняя кинетическая энергия молекул газа возрастет (станет пропорциональна kТ₂), суммарная кинетическая энергия всех частиц газа возрастет, а внут­ренняя энергия частиц некоторое время будет оставаться неизменной. В результате неупру­гиx соударении, при которых часть кинетической энергии молекул переходит во внyтpeн­нюю энергию частиц, произойдет ее увеличение так, что установится новое распределение частиц по энергиям. После установления нового равновесия внутренняя энергия распредел­яeтся по закону Больцмана при температуре Т_2. Постоянная времени установления процесса релаксации называется временем релаксации .

Релаксационные процессы происходят не только в газах, но и в твердых телах. Переход кинeтической энергии одной частицы во внутреннюю энергию другой при неупругих столк­новениях молекул газа служит примером релаксационных переходов. Последние носят ста­тистический характер. Вероятности релаксационных переходов между уровнями Е₁ и Е₂ бу­дем обозначать E₁₂, а обратных переходов Е₂₁. В большинстве случаев, имеющих место в квантовых приборах, релаксационные переходы являются безызлучательными.

В состоянии термодинамического равновесия населенности уровней не изменяются во времени, поэтому число безызлучательных переходов с уровня 1 на уровень 2 в 1 с равно числу обратных безызлучательных переходов с уровня 2 на уровень 1:

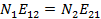. (3.16)

В состоянии термодинамического равновесия распределение населенностей определяет­ся законом Больцмана. Получаем

(3.17)

Из этого следует, что вероятность безызлучательных переходов сверху вниз больше, чем снизу вверх (Е₂₁ > E₁₂) в отличие от вероятностей вынужденных переходов, которые одинаковы. Если , что обычно справедливо для квантовых приборов СВЧ-диапа­зона, то (3.17) можно заменить приближенным выражением

(3.18)

Поиск по сайту: