 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Туннельный эффект
Рассмотрим случай одномерного движения частицы вдоль оси х, когда потенциальная энергия U меняетсяскачком в одной точке 0. При х < 0 U= 0, а при x > 0 она равна постоянному значению U0, как это показано на рис. 1.3. Эта ситуация соответствует сильно урезанному одномерному потенциальному ящику, одна стенка которого в процессе урезания утратилась совсем, а вторая имеет маленькое конкретное значение и не равна бесконечности. График зависимости потенциальной энергии от координаты х (потенциальная кривая) имеет вид ступеньки высотой U0и называется потенциальной стенкой.Вдоль осей у и zпотенциальная энергия не меняется.
Неквантовая картина движения в этом поле такова: если полная энергия частицы ε < U0, то частица, движущаяся слева направо, достигнет потенциальной стенки (в точке А) и отразится от нее. Проникнугь в область х > 0 частица не смогла бы никогда и ни при каких обстоятельствах, так как при этом ее полная энергия Е, равная соотношению 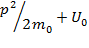 (которая в силу закона сохранения энергии остается неизменной), оказалась бы меньше потенциальной, так что при этом импульс
(которая в силу закона сохранения энергии остается неизменной), оказалась бы меньше потенциальной, так что при этом импульс 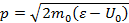 стал бы чисто мнимым. Потенциальная стенка подобна абсолютно твердой стенке.
стал бы чисто мнимым. Потенциальная стенка подобна абсолютно твердой стенке.
В квантовой механике нахождение частицы внутри области ε < U не приводит к бессмысленному выводу об отрицательной кинетической энергии. Кинетические и потенциальные энергии согласно соотношению неопределенностей не имеют одновременно точных значений, так как кинетическая энергия зависит от импульса, а потенциальная энергия - от координаты. Поэтому равенство Е = р2/2т + Uимеет в квантовой механике лишь тот смысл, что в любом состоянии средняя полная энергия равна сумме средней кинетической и средней потенциальной энергий.
Согласно квантовой механике волновая функция частицы, движущейся к стенке с импульсом  , представляет собой в этой области плоскую волну де Бройля. При x
, представляет собой в этой области плоскую волну де Бройля. При x  полная энергия та же, что и при х < 0, но теперь в выражении для плоской волны вместо
полная энергия та же, что и при х < 0, но теперь в выражении для плоской волны вместо  , должна стоять следующая величина:
, должна стоять следующая величина:
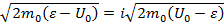 . (1.28)
. (1.28)
| A |
| E |
| U0 |
| U |
| x |
| Рис. 1.3. Потенциальная ступенька высотой U0 |
| Re Ψ |
Эту величину уже нельзя истолковать как импульс частицы. Зависимость волновой функции от времени при х < 0 и х> 0 одна и та же, но зависимость от координат при х> 0 становится апериодической:
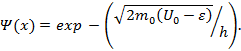 (1.29)
(1.29)
Волновая функция при х > О экспоненциально убывает с ростом х, как это показано на рис. 1.3. В пространстве перед потенциальной стенкой наряду с падающей волной существует и отраженная волна. При этом волновые функции перед стенкой (х < 0) и внутри нее (х > 0) связаны друг с другом, поскольку волновая функция не может прерываться. В точке х = О значения волновых функций и значения их производных по координате должны совпадать вследствие непрерывности волновой функции и ее первой производной.
Согласно зависимости (1.29) имеется конечная вероятность обнаружения частицы в классически запрещенной области х > 0. Эта вероятность экспоненциально убывает с увеличением координаты х. Убывание происходит тем быстрее, чем значительнее потенциальная энергия U0превышает полную энергию частицы ε. Вероятность обнаружения частицы на расстояниях, намного больших длины волны де Бройля, мала. Возможность проникновения частицы в классически запрещенную область дает ключ к пониманию многих процессов, существование которых с точки зрения классической механики необъяснимо. Рассмотрим простую задачу. Допустим, имеется узкая область шириной а, внутри которой потенциальная энергия равна U0. Вне этой области потенциальная энергия равна нулю. Потенциальная кривая имеет вид барьера прямоугольной формы (рис. 1.4), называемого потенциальным барьером. Частица с энергией ε < U0, движущаяся слева направо, согласно классической механике не может преодолеть этот барьер и отражается от него.
| a |
| x |
| U0 |
| U |
| Рис. 1.4. Прямоугольный потенциальный барьер |
| ε |
| Re Ψ |
Волновая функция при x> а также представляет собой волну де Бройля той же частоты (так как энергия частицы остается прежней), но с гораздо меньшей амплитудой, чем перед барьером, как это показано на рис. 1.4. Возникает физическое явление проникновение частиц сквозь потенциальный барьер, получившее название туннельный эффект.
Вероятность обнаружения частицы в точке х пропорциональна квадрату модуля волновой функции 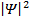 . Поэтому отношение двух таких величин, как вероятность найти частицу за барьером в точке х = а и вероятность обнаружения частицы перед барьером в точке х = 0, согласно выражению (1.29) имеет вид
. Поэтому отношение двух таких величин, как вероятность найти частицу за барьером в точке х = а и вероятность обнаружения частицы перед барьером в точке х = 0, согласно выражению (1.29) имеет вид
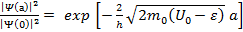 . (1.30)
. (1.30)
Это отношение определяет вероятность «просачивания» частицы сквозь барьер и называется коэффициентом прохождения частицы через потенциальный барьер.Главная особенность формулы (1.30) заключается в том, что очень малая по сравнению с остальными ингредиентами величина - постоянная Планка - стоит в знаменателе экспоненты. Вследствие этого коэффициент прохождения через барьер для классической частицы, обладающей большой массой, чрезвычайно мал. Но чем меньше масса частицы, тем больше и вероятность туннельного эффекта.
Например, при высоте барьера 2 эВ и ширине 10-8 см вероятность прохождения сквозь барьер для электрона с энергией 1 эВ равна 0,78, а для протона с той же энергией - только 3,6·10-19 (очень маленькой величине). Если же взять макроскопическое тело - шарик массой 1 г, движущийся по горизонтальной поверхности с очень маленькой скоростью (кинетическая энергия близка к нулю), то вероятность преодоления им препятствия - лезвия бритвы толщинoй 0,1 мм, выступающего над горизонтальной поверхностью на 0,1 мм, равна 10-26, но не равна нулю.
Прохождением частиц сквозь потенциальный барьер объясняется ионизация атомов в сильном электрическом поле, вырывание электронов из металла под действием электрического поля (автоэлектронная эмиссия) и многие другие удивительные явления. На использовании туннельного эффекта основано действие такого мощного аналитического прибора, как сканирующий туннельный микроскоп (позволяющий проводить экспериментальные исследования на атомарном уровне) и многих других приборов, разработанных в последнее время с помощью нанотехнологии для целей нанотехнологии и относящихся к области наноэлектроники и оптоэлектроники.
Поиск по сайту: