Волновые свойства свободных частиц

Можно попытаться получить решение уравнения Шредингера для случаев, когда известно силовое поле, характеризующееся потенци­альной функцией U (х). Как и при использовании законов Ньютона, простейшая ситуация складывается в случае, когда сила, действую­щая на частицу, равна нулю. Предположим, что U (х) = 0 и исследу­ем уравнение Шредингера. Уравнение (1.13) принимает вид

(1.15)

Уравнение (1.15) оказывается чрезвычайно простым, поскольку оно имеет тот же вид, что и уравнение, описывающее гармониче­ский осциллятор, если время в этом уравнении заменить на х. Решениями такого уравнения является синус или косинус неко­торого аргумента, однако по ряду соображений более удобна эк­споненциальная форма. Одним из решений (но не самым общим) является функция вида

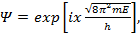(1.16)

а зависящая от времени Ψ-функция приобретает вид

. (1.17)

Функция (1.17) описывает бегущую волну.

Для подтверждения того, что функция (1.17) носит характер бегущей волны, рассмотрим струну, колеблющуюся со смещени­ем в направлении у, которое определяется из выражения

Смещение струны в момент времени t равно e^ikx, т. е. выражает­ся синусоидой с длиной волны 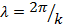. Движение точки в начале координат х = О описывается выражением е^iшt, которое также пред­ставляет собой синусоиду с периодом . Постоянная k назы­вается вектором распространения, или волновым вектором, а ω ­угловой частотой. Очевидно, что в другой момент времени в дру­гой точке колебание струны также является синусоидальным, но его фаза сдвинута относительно фазы первоначального колебания. Волна распространяется вдоль струны со скоростью 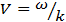, по­скольку в момент времени t смещение (или фаза), находившееся в точке х = 0 при t=0, сместилось в точку .

Функция Ψ в уравнении (1.17) имеет тот же вид, что и волна в струне, и, таким образом, можно прийти к выводу, что волновая функция для частицы представляет собой бегущую волну. Этот вывод является полезным сам по себе, но, кроме того, с помо­щью простых преобразований из формулы (1.17) можно получить два очень важных соотношения. Запишем сначала эту формулу в виде

(1.19)

Здесь частота выражается через энергию системы.

. (1.20)

Постоян­нaя k является также функцией энергии:

.

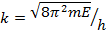Представим k в другом виде. Так как энергия в рассматривае­мом случае является кинетической энергией U(x)=0, то , где p- импульс частицы. Таким образом,

(1.21)

Соотношение (1.20), называемое соотношением Эйнштейна, и соотношение (1.21), называемое соотношением де Бройля, ус­танавливают, что движение частицы носит волновой характер. Они представляют собой концепцию корпускулярно- волнового дуализ­ма. Сущность его можно выразить следующим образом. Волновая функция электрона, если на него не действуют силы, представля­ет собой бегущую синусоидальную волну, но если электрон ка­ким-либо образом обнаруживается в действительности, то он об­наруживается как реальная и вполне локализованная частица.

Поиск по сайту: