Волновая функция

Необходимость вероятностного подхода к описанию каждой из элементарных частиц относится к любым процессам в микромире и является одной из важнейших отличительных особенностей кван­товой теории. Можно ли истолковать волны де Бройля непосред­ственно как волны вероятности, т. е. правильно ли считать, что вероятность обнаружения микрочастицы в разных точках простран­ства меняется по волновому закону? Нет, поскольку если вероят­ность меняется по волновому закону, то тогда вероятность обна­ружения частицы для некоторых точек пространства примет от­рицательные значения, что противоречит ее смыслу.

Эти трудности можно устранить, если принять, что по волно­вому закону меняется не сама вероятность, а некая величина, названная амплитудой вероятности и обозначаемая обычно Ψ(x,y,z,t). Эту величину называют также волновой функцией. Амплитуда вероятности должна быть комплексной, а вероятность ω должна быть пропорциональна квадрату ее модуля:

(1.6)

Волновая функция выступает в квантовой теории как основ­ной носитель информации и о корпускулярных, и о волновых свойствах системы. Вероятность dω нахождения частицы в элемен­те объема dVравна:

dω= ,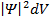

поэтому величину 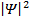называют плотностью вероятности (т. е. ве­роятностью, отнесенной к единице объема). Предложенное Мак­сом Борном толкование волн де Бройля исключает их понимание как классических волн материи. Связывая со свободным электро­ном плоскую волну, не следует это понимать (по Борну), что элек­трон будто бы «размазан» по огромной области. Это означает, что хотя электрон продолжает выступать в теории как точечный объект, вероятность обнаружения его в любой из точек пространства одинакова.

Описывающая состояние квантовой частицы волновая функ­ция Ψ не может быть непосредственно измерена, хотя выражаю­щиеся через Ψ физические величины являются объектами экспе­риментальных исследований.

По установившейся терминологии некоторое математическое действие, производимое над величиной, рассматривается как ре­зультат применения к этой величине определенного оператора. В квантовой механике, как правило, встречаются линейные и квад­ратичные зависимости от импульса. Квадрат оператора понимает­ся как знак двукратно повторенного действия этого оператора. Как и в любой теории, дающей вероятностное описание, сопоставление с опытом про изводится для средних значений физиче­ских величин. В квантовой механике вводится важный постулат: каж­дой физической величине, выражаемой в классической механике в виде определенной функции F(x,y,z,p_x,p_y,p_z)координат и импуль­сов, ставится в соответствие оператор . Такое сопоставление операторов с классическими величинами является общей специфической чертой квантования.

Если действие оператора на волновую функцию Ψ равно­сильно ее умножению на некоторое число а, то Ψ называют соб­ственной функцией оператора, а число а- его собственным зна­чением:

(1.7)

Конкретному оператору соответствует определенное множество собственных функций и собственных значений. Совокупность соб­ственных значений называют их спектром.Таким образом, наблю­даемые на опыте значения физических величин и есть собствен­ные значения для операторов соответствующих величин. Это по­ложение считается настолько важным, что его часто рассматрива­ют как отдельный постулат квантовой механики.

Если собственные значения меняются плавно (непрерывно), т. е. могут пробегать любые промежуточные значения, то их спектр называют непрерывным. Однако наиболее интересным и специ­фичным именно для квантовой теории является существование дискретных спектров, которые нельзя объяснить на основе клас­сической физики. Появление такой дискретности обусловливает­ся чаще всего видом операторов физических величин и граничны­ми условиями.

Поиск по сайту: